Is there a specific reason to typecast to np.float32 as below
cum_counts = counts.astype(np.float32).cumsum(axis=0)
Would it matter if we had it
cum_counts = counts.cumsum(axis=0)
Is there a specific reason to typecast to np.float32 as below
cum_counts = counts.astype(np.float32).cumsum(axis=0)
Would it matter if we had it
cum_counts = counts.cumsum(axis=0)
This is for float division in
estimates = cum_counts / cum_counts.sum(axis=1, keepdims=True)
Without typecase, it will be int division.
Thanks for the help !!!
Hi @HyuPete, @rammy_vadlamudi, @randomonlinedude! Sorry for the delay reply, I totally agree with your stand after careful calculations. We may adjust the narration of this question. Thanks for the feedback!
@zplovekq, @HyuPete
The error here is to assume both trials of the same test would be independent like throwing a dice multiple times. Probabilities given in table 2.6.1 assumes you are a “generic” individual. But P(D1_2) is not independant to P(D1_1) (where in P(Dx_y), x is the test and y the trial) if you are the same person. Assume that a certain a certain gene is the cause for false positive with test 1, running the test again should not give you a different result.
Now the exercise assumes that D1 and D2 are independent, that is, whatever reason you have false positive in D1 has no impact on D2 and vice versa. But that assumption cannot be made if you run the same test twice on the same person.
To make a programming analogy, that would be like running a unit test multiple times hoping it’ll catch a bug that is not covered by the test.
Sorry if this explanation has already been expanded here.
I think the main reason not using twice the same test is that one of the Bayes condition, mean, independancy of diagnostics, should no longer available.
Then, following formula should no more available :
P(H=1 | D1=1, D2=1) = P(D1=1, D2=1 | H=1) *P(H=1) / P(D1=1, D2=1)
Check the requirement of P(A & C) = P(A)P©, which requires the independence between A and C
i saw table and couldn’t understand P(D2 =1|H=1) = 0.98? Can you explain for me?
You can search the keyword: Conditional probability for more detail.
Here I will explain the meaning of this formula
P(D2 =1|H=1) = 0.98 means the probability of D2 = 1 happens given that H = 1 is 0.98. It is the compensation of P(D2=0|H=1) = 0.2. You can think like this: when H=1 happens, there is only 2 senarios occur:
D2 =1 (0.98)D2 = 0 (0.02)Assuming that 2 events are independent ->
Answer: To find a probability of P_(P(A), P(B | A), P(C | B)) == p_(P(A) x P(B | A) x P(C | B))
please could you write the code because it’s unreadable
# task 2.6
import seaborn as sns
import warnings
warnings.filterwarnings(‘ignore’)
def plot_distrib(distribution, sample, mx, nx):
plt.figure(figsize=(4, 3), dpi=80)
sns.distplot(distribution, color=‘red’, label=‘True distribution’)
sns.distplot(sample, color=‘blue’, label=‘True distribution’)
plt.title(f’True and Sampel distr. with dist size {mx} and sample size {nx}’)
plt.legend(loc=‘right’)
plt.show();
nx = [50, 100]
mx = [300, 500]
for m in mx:
for n in nx:
distribution = np.random.normal(size=m)
sample = np.random.choice(distribution, size=n)
plot_distrib(distribution, sample, m, n)
What is the best way to remember all the probability equations? Also, are the equations associated with probability necessary for software developing/coding?
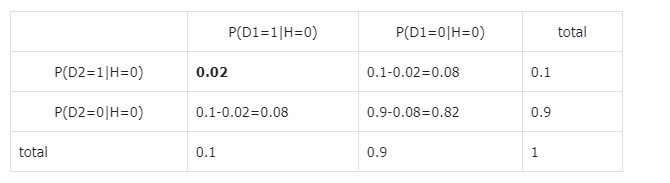
How to calculate the joint table in part 1 of exercise 7? If I was right, we have to calculate $P(D_1 = 0, D2=0 | H = 0)$ and $P(D_1 = 0, D2=1 | H = 0)$ and $P(D_1 = 1, D2=0 | H = 0)$ right?