Probability

English Version mxnet
1

http://d2l.ai/chapter_preliminaries/probability.html

2

I have the question on Exercises 4:Why not just run the first test a second time?
I think it just like roll a die twice. The two result is independent. So by the same formula, i have the result P(H = 1 | D1 = 1, D2 = 1)=0.0015/0.00159985=93%. This is better.
Looking forward for discuss!

3

Hi @zplovekq, $P(H = 1, D1 = 1, D2 = 1)$ is not equal to 0.0015, since in the second test some true positive cases are tested as negative.

4

Thanks for your reply!~
I compute P(H = 1, D1 = 1, D2 = 1) by this:
P(D1 = 1, D2 = 1 | H = 1)=P(D1 = 1 | H = 1)P(D2 = 1 | H = 1)=11=1 (Because it just like roll a die twice, i think the two diagnosis is independent).
Then P(D1 = 1, D2 = 1)=P(D1 = 1, D2 = 1 | H = 0)P(H = 0) + P(D1 = 1, D2 = 1 | H = 1)P(H = 1)
=0.010.01*(1-0.0015)+1*0.0015=0.00159985
So if the two diagnosis are all 1, then:
P(H = 1 | D1 = 1, D2 = 1)= $P(D1 = 1, D2 = 1 | H = 1)P(H = 1) / P(D1 = 1, D2 = 1)$
= 1 * 0.0015/0.00159985=93%
Thus i think use the first test twice will have more accurate.
Is there any thing wrong?
Thanks!

1 Like
5

This is not equal to 1. It is 0.98, as the table says.

6

emm…Thanks for reply!
I mean use the first test twice…So i think P（D2 = 1 | H = 1）= P（D1 = 1 | H = 1）=1…

7

Hi @zplovekq, no problem at all!

1 Like
8

I have the same thought as you. Still don’t know the answer to this question :thinking:

9

The question suggests that D2 is the same as D1. So I think P(D2 = 1 | H = 1) = P(D1 = 1 | H = 1) = 1.
Is there any thing wrong with my intuition?

10

Hi @HyuPete, please see my previous response.

Let me know if it doesn’t make sense to you.

11

I think I should give more details here so you can help me figure out my problem.
First, let me quote the question here:

  1. In Section 2.6.2.6, the first test is more accurate. Why not just run the first test a second time?

Now here are my thoughts:

  1. In the reading section, it states that D2 is different from D1.

    The second test has different characteristics and it is not as good as the first one, as shown in Table 2.6.2.

    I totally agree that in the reading section, P(D2 = 1 | H = 1) = 0.98, as you said.

    I also want to briefly recall this reading section here:

    • First time: run first test D1.

    • Second time: run second test D2.

    • The the probability of the patient having AIDS given both positive tests is:
      P(H = 1 | D1 = 1, D2 = 1) = … = 0.8307.

  2. Go back to the question, it says “run the first test a second time”. So my understanding is D2 is now the same as D1. I think you have misunderstood what I said because of my abuse of notation. So let me correct it:

    • First time: run first test D1, call this run as D^(1)_1.
    • Second time: run first test D1 again, call this run as D^(2)_1.
    • P(D^(1)_1 | H = 1) = P(D^(2)_1 | H = 1) = 1.

    And my calculation for this case, “the probability of the patient having AIDS given both positive tests is”:

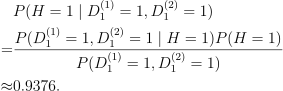
  3. Since 0.9376 > 0.8307, I think “run the first test a second time” is a better choice here. But the question is “Why not just run the first test a second time?” which leads to a conflict.

Therefore, I still don’t know how to answer this question. Hope you could guide me to it.
Thanks in advance for your help.

12

Help me too.:face_with_raised_eyebrow:

13

np.random.multinomial(10, fair_probs), is not working, its giving result array([ 0, 0, 0, 0, 0, 10], dtype=int64) also the code counts = np.random.multinomial(1000, fair_probs).astype(np.float32)
counts / 1000, Giving results array([ 0., 0., 0., 0., 0., 1000.]). There is a error in np lib of mxnet please check

14

@Prateek_Vyas
You’re right. Win10?
Check: https://discuss.mxnet.io/t/probability-np-random-multinomial/5667/6
issue: https://github.com/apache/incubator-mxnet/issues/15383
Wait for fixing…@mli

15

Thanks for reporting @Prateek_Vyas. The fix should be on 2.0 roadmap.

1 Like
16

@goldpiggy Please help me.

17

@goldpiggy, could anyone shed some light on @HyuPete view …

18

@HyuPete is using table 1 values for both event’s D1 and D2 where as the reading section uses this second table to calculate p(H=1 | D1=1 , D2=1), which bring us at different answers …

So the question why the 2nd table differ from 1st, if both are completely independent event ?

@goldpiggy

image
image865×191 6.77 KB

19

Is there a specific reason to typecast to np.float32 as below

cum_counts = counts.astype(np.float32).cumsum(axis=0)

Would it matter if we had it
cum_counts = counts.cumsum(axis=0)

20

This is for float division in
estimates = cum_counts / cum_counts.sum(axis=1, keepdims=True)

Without typecase, it will be int division.