Probability

English Version mxnet
7

Hi @zplovekq, no problem at all!

1 Like
8

I have the same thought as you. Still don’t know the answer to this question :thinking:

9

The question suggests that D2 is the same as D1. So I think P(D2 = 1 | H = 1) = P(D1 = 1 | H = 1) = 1.
Is there any thing wrong with my intuition?

10

Hi @HyuPete, please see my previous response.

Let me know if it doesn’t make sense to you.

11

I think I should give more details here so you can help me figure out my problem.
First, let me quote the question here:

  1. In Section 2.6.2.6, the first test is more accurate. Why not just run the first test a second time?

Now here are my thoughts:

  1. In the reading section, it states that D2 is different from D1.

    The second test has different characteristics and it is not as good as the first one, as shown in Table 2.6.2.

    I totally agree that in the reading section, P(D2 = 1 | H = 1) = 0.98, as you said.

    I also want to briefly recall this reading section here:

    • First time: run first test D1.

    • Second time: run second test D2.

    • The the probability of the patient having AIDS given both positive tests is:
      P(H = 1 | D1 = 1, D2 = 1) = … = 0.8307.

  2. Go back to the question, it says “run the first test a second time”. So my understanding is D2 is now the same as D1. I think you have misunderstood what I said because of my abuse of notation. So let me correct it:

    • First time: run first test D1, call this run as D^(1)_1.
    • Second time: run first test D1 again, call this run as D^(2)_1.
    • P(D^(1)_1 | H = 1) = P(D^(2)_1 | H = 1) = 1.

    And my calculation for this case, “the probability of the patient having AIDS given both positive tests is”:

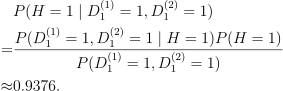
  3. Since 0.9376 > 0.8307, I think “run the first test a second time” is a better choice here. But the question is “Why not just run the first test a second time?” which leads to a conflict.

Therefore, I still don’t know how to answer this question. Hope you could guide me to it.
Thanks in advance for your help.

12

Help me too.:face_with_raised_eyebrow:

13

np.random.multinomial(10, fair_probs), is not working, its giving result array([ 0, 0, 0, 0, 0, 10], dtype=int64) also the code counts = np.random.multinomial(1000, fair_probs).astype(np.float32)
counts / 1000, Giving results array([ 0., 0., 0., 0., 0., 1000.]). There is a error in np lib of mxnet please check

14

@Prateek_Vyas
You’re right. Win10?
Check: https://discuss.mxnet.io/t/probability-np-random-multinomial/5667/6
issue: https://github.com/apache/incubator-mxnet/issues/15383
Wait for fixing…@mli

15

Thanks for reporting @Prateek_Vyas. The fix should be on 2.0 roadmap.

1 Like
16

@goldpiggy Please help me.

17

@goldpiggy, could anyone shed some light on @HyuPete view …

18

@HyuPete is using table 1 values for both event’s D1 and D2 where as the reading section uses this second table to calculate p(H=1 | D1=1 , D2=1), which bring us at different answers …

So the question why the 2nd table differ from 1st, if both are completely independent event ?

@goldpiggy

image
image865Ă—191 6.77 KB

19

Is there a specific reason to typecast to np.float32 as below

cum_counts = counts.astype(np.float32).cumsum(axis=0)

Would it matter if we had it
cum_counts = counts.cumsum(axis=0)

20

This is for float division in
estimates = cum_counts / cum_counts.sum(axis=1, keepdims=True)

Without typecase, it will be int division.

21

Thanks for the help !!!

22

@HyuPete Im on the same boat with you, I got the same result and could not get the answer @@

1 Like
23

Hi @HyuPete, @rammy_vadlamudi, @randomonlinedude! Sorry for the delay reply, I totally agree with your stand after careful calculations. We may adjust the narration of this question. Thanks for the feedback!

2 Likes
24

@zplovekq, @HyuPete
The error here is to assume both trials of the same test would be independent like throwing a dice multiple times. Probabilities given in table 2.6.1 assumes you are a “generic” individual. But P(D1_2) is not independant to P(D1_1) (where in P(Dx_y), x is the test and y the trial) if you are the same person. Assume that a certain a certain gene is the cause for false positive with test 1, running the test again should not give you a different result.

Now the exercise assumes that D1 and D2 are independent, that is, whatever reason you have false positive in D1 has no impact on D2 and vice versa. But that assumption cannot be made if you run the same test twice on the same person.

To make a programming analogy, that would be like running a unit test multiple times hoping it’ll catch a bug that is not covered by the test.

2 Likes
25

Sorry if this explanation has already been expanded here.

I think the main reason not using twice the same test is that one of the Bayes condition, mean, independancy of diagnostics, should no longer available.

Then, following formula should no more available :

P(H=1 | D1=1, D2=1) = P(D1=1, D2=1 | H=1) *P(H=1) / P(D1=1, D2=1)

26

Check the requirement of P(A & C) = P(A)P©, which requires the independence between A and C

1 Like