Chap 5.2.2.1
in the first and second pytorch code, for function
init_normal(m)
I guess it should be
nn.init.XXX(m.weight, *args)
since
pytorch.nn.Module.apply(fn) Applies `fn` recursively to every submodule (as returned by
.children()) as well as self.
it doesn’t make sense to repeatedly initialize net[0] and it’s aiming to initialize all parameters
Hi @kwang that’s a great catch. If we are to apply initialization to all the Linear layers in the network, then we should replace net[0] to m inside the init_normal function.
Ps. While I was at it, I have fixed the naming of the functions too. The second function should be named init_constant.
This is now fixed in master. You can soon see the changes in the next update to release branch.
Thanks!
For tied parameters (link), why is the gradient the sum of the gradients of the two layers? I was thinking it would be the product of the gradients of the two layers. Reasoning:
y = f(f(x))
dy/dx = f’(f(x))*f’(x) where x is a vector denoting the shared parameters.
Maybe the grad of the shared layer is not reset to 0 after the first time we meet it, so the grad of the shared layer would be computed twice and the final grad would be the sum?
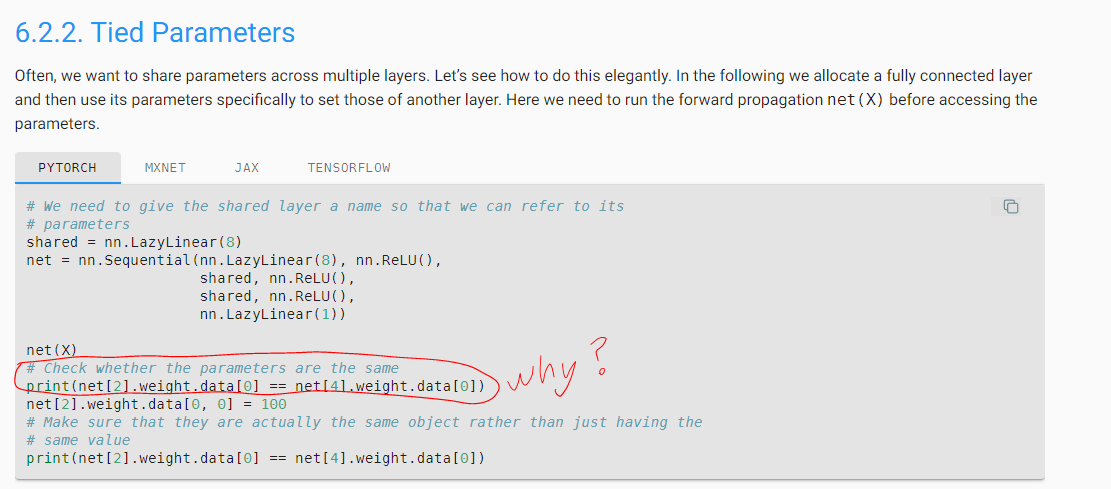
For tied parameters 5.2.3 print(net[2].weight.data[0] == net[4].weight.data[0]), I am guessing it should have been print(net[2].weight.data[0] == net[3].weight.data[0]), given parameters are shared among layer 2 and layer 3.
Layer 2 and Layer 3 have a ReLU between them
therefore
net[3]
would index the ReLU
that is why its
I have a doubt in the “Custom Initialization section”.
def my_init(m):
if type(m) == nn.Linear:
print(
"Init",
*[(name, param.shape) for name, param in m.named_parameters()][0])
nn.init.uniform_(m.weight, -10, 10)
m.weight.data *= m.weight.data.abs() >= 5
net.apply(my_init)
net[0].weight[:2]
where is the probability thing implemented in thecode given in the book?
If you see it closely, this is already incorporated. The values between -5 and 5 have a probability of 0.5 to occur and those are being converted to 0.
m.weight.data.abs() >= 5
This return True(or 1) if it is true and False(0) if 0 if it is false and it is being taken care here.
If anyone else is wondering why the weight matrices are transposed in layers, e.g. the shape of the weights of nn.Linear(4, 8) prints torch.Size([8, 4]) in the beginning.
It seems to be an optimization, because when multiplying from the right by the W weight matrix, we would iterate columns, which is cache-inefficient:
https://discuss.pytorch.org/t/why-does-the-linear-module-seems-to-do-unnecessary-transposing/6277/5
Instead of making multiple init functions, I tried to make just one like this:
def init(m, init_type = 'normal', constant = 1):
if type(m) == nn.Linear:
if init_type == 'normal':
nn.init.normal_(m.weight, mean=0, std=0.01)
nn.init.zeros_(m.bias)
elif init_type == 'xavier':
nn.init.xavier_uniform_(m.weight)
elif init_type == 'constant':
nn.init.constant_(m.weight, constant)
nn.init.zeros_(m.bias)
Then I can use the init function like this:
init(net[0], init_type = 'normal')
init(net[2], init_type = 'xavier')
In regards to code snippet in 6.2.2. Comparing tensors by printing them out can work as a quick and dirty way of doing it for (very) small experiments. You can keep it if you really want to display the output visually for the reader here, but you should really be showing students how to use an assert as well. There may be a more sexy way of doing it without explicitly flattening the tensors and converting them to a native list, but something like this kinda shows what I mean, and it works fine here:
assert(list(net[2].weight.data[0].ravel()) == list(net[4].weight.data[0].ravel()))
