Numerical Stability and Initialization

English Version mxnet
1

http://d2l.ai/chapter_multilayer-perceptrons/numerical-stability-and-init.html

2

I’d just like to point out a small mistake in the book: In the subsection discussing Xavier Initialization, the variance of h_i is noted as E[h_i] rather than Var[h_i]. This error is also made with the variances of W_ij and x_ij. It’s just a small notational error, but one that some readers (including yours truly) may find a bit confusing.

3

Hi @jackrcole, great catch! We will fix it!

1 Like
4

Why is \partial_{W^{(l)}} h^{(l)} in formula 4.8.2. a vector? In my opinion, it has to be a 3rd level tensor. Two indices from W^{(l)} and one index from h^{(l)}. So, the right side is a tensor 3rd level. This is in agreement with the left side (also a 3rd level tensor). In another formulation, W is flattened to a vector to get (on the left and right side) Jacobian matrices.

1 Like
5

Hi @chris_elgoog, I believe you are correct! Would you like to be a contributor to D2L and make a PR for the typo? Thanks!

6

Thanks for the reply. I made a pull request as suggested.

7

Seems like this is still not fixed?

8

Can you share the implementation of Xavier Initialization on PyTorch? Thanks in advance.

9
  1. Look up analytic bounds on the eigenvalues of the product of two matrices. What does this
    tell you about ensuring that gradients are well conditioned?

I guess any individual big values that comes out of the range, might be a sign of some numerical instability.

10
  1. If we know that some terms diverge, can we fix this after the fact? Look at the paper on
    layer-wise adaptive rate scaling for inspiration

For example, you can increase the size of the batch, and dynamically adapt the learning rate for each layer. in fact, at mentioned article was proposed that approach based on empirical experiments with data.

11

What the hell is this? I cannot understand.
wtf

12

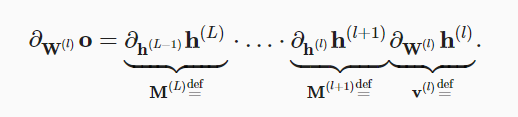
def xavier_initialization(layers):
params = []
for i in range(len(layers)-1):
a = math.sqrt(6/(layers[i] + layers[i+1]))
params.append(torch.tensor(np.random.uniform(-a, a, (layers[i], layers[i+1])), dtype=torch.float32, requires_grad=True))
#params.append(torch.Tensor((layers[i], layers[i+1]), requires_grad=True).uniform_(-a, a))
params.append(torch.tensor(np.random.uniform(-a, a, (layers[i+1])), dtype=torch.float32, requires_grad=True))
#params.append(torch.randn(layers[i+1], dtype = torch.float32, requires_grad=True))
return params