this code all_items = set([i for i in range(**num_users**)]) should be
all_items = set([i for i in range(**num_items**)])
For each user, the items that a user has not interacted with are candidate items (unobserved entries). The following function takes users identity and candidate items as input, and samples negative items randomly for each user from the candidate set of that user.
Here, in the context, the words “candidate items” indicate unobserved items for a user. However, this is contradictory with the code, where the variable “candidates” indicate the rated items for a user.
auc = 1.0 * (max - hits_all[0][0]) / max if len(hits_all) > 0 else 0
How does this formula correspond to the auc definition metioned above in the context?
Maybe you can check the way the authoer loads the train_iter/test_iter, which is in the mode ‘seq_ware’ . So actually when we do loop in users, each time we query the user’s most recent behaviour in the test_iter(a key-val dictionary) and then the result list(which length is one and conatins the item_id) is passed to the evaluate function. Moreover, in the hit_and_auc function we try to find whether the item the net “recommend” is in the top-k list or what’s the rank of that “recommendation” in the hits_al list(which is sorted by the score given by the net),which is corresponding to the way we calculate the AUC (find out how many false recommendations rank before the ground truth)
Why is the hadamard product used in the GMF?
From what I recall, a Matrix Factorization is defined as multipliying two matrices, usually of lower rank as the target matrix, using usual matrix multiplication, i. e. trying to reconstruct X as X’ = A \dot B with some reconstruction error. Is there some additional information available on this?
In the original paper, they wanna add some nonlinear layers over the dot product so they used element-wise multiplication in order to get a vector.
X’ = A \dot B is seen from the whole matrix level. If we look at it from each recommendation level, we need a score for each user-item pair. So that is vector-vector multiplication instead of matrix multiplication. Hope this helps.
Thank you, this is a good answer.
Is it correct that there is a sigmoid activation in the last layer given that the BPR loss then applies a sigmoid again?
Hi!The definition of PRDataset may not be good enough. neg_items can be pre-calculated once during initialization.
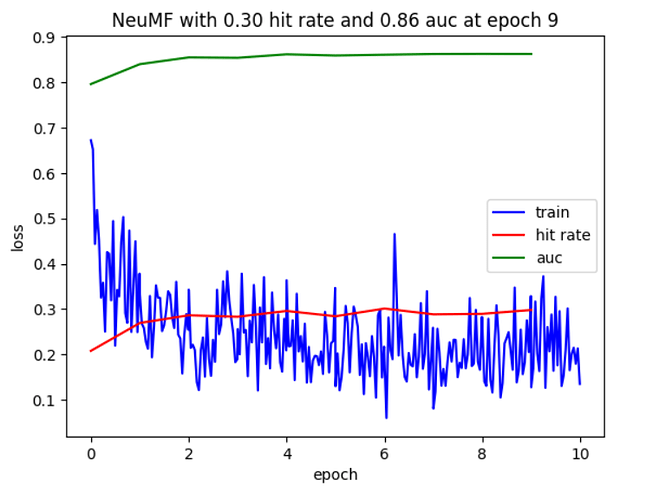
Why are the AUC and hit rate curves horizontal lines during training? It doesn’t make sense to me.
Note: The code I implemented is in PyTorch
First: What is the purpose of a sigmoid function at the prediction layer? I got better results by removing it. The reason I removed Sigmoid was that it did not allow the predictive distance between the positive and negative samples to increase, which caused the loss function to not decrease as expected.
Second: How come your model isn’t improving the HIT and AUC metrics with each epoch?
Third (Note: I am not familiar with MXNET syntax): Why does your BRPLoss seem so low? Here are my thoughts. According to your code, you are not implementing batch optimization. This means you are computing loss, gradient, weight updating, etc., for each sample in each batch. And finally in the epoch reports, you average the loss functions which is inconsistent with the book definition of BPRLoss.
My final epoch report without sigmoid in prediction layer:
----- epoch number 9/10 -----
training loss is: 337.0008469414465
hit rate is: 0.1951219512195122
AUC is: 0.7946674890472771
----- epoch number 10/10 -----
training loss is: 335.34528846347456
hit rate is: 0.19618239660657477
AUC is: 0.7952683387070411I’m getting that the AUC is 0.531 which is a very low score - I think the neural net isn’t converging properly. I’ll do some fiddling with the parameters to get it to converge.