https://d2l.ai/chapter_appendix-mathematics-for-deep-learning/multivariable-calculus.html
In code section 18.4.6 should the indexing = 'xy'
x, y = np.meshgrid(np.linspace(-2, 2, 101),
np.linspace(-2, 2, 101), indexing=‘ij’)
z = x*np.exp(- x2 - y2)
as xy represents cartesian coordinates? Although in the above example it should not matter as x and y for the meshgrid are same.
Hi @sushmit86, great question! I believe it should be an “ij” here. According the NumPy document:
In the 2-D case with inputs of length M and N, the outputs are of shape (N, M) for ‘xy’ indexing and (M, N) for ‘ij’ indexing.
Let me know if it makes sense to you.
Thanks for the explanation.
Hello, I have trouble interpreting the formula at 18.4.2. I understand the part before it under 18.4.1. and how this is basically the application of the last equation under 18.3.6, which shows that a small increase of a function is a sum of the original function plus the small increase times the function’s derivative. However, I don’t understand where the following term comes from and how to interpret it: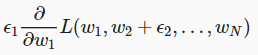 
. I also don’t understand how this term is subsequently rewritten into the last two terms of the following equation.
As far as I understand the partial derivative, you simply calculate the derivative while keeping all other variables constant. However, here we are adding a small quantity to w2 whilst we are calculating the partial derivative of w1.
Especially where the product of epsilon 1 and 2 comes from confuses me, but I’m pretty confused overall. Any clarification would be greatly appreciated.
Hey @GFlow, great question! Actually there is a small typo here and there should be an “epsilon_N” behind the “w_N”. I just fixed it in this PR.
For the following equation, we just need to take out the “epsilon_2” out from 
and 
.
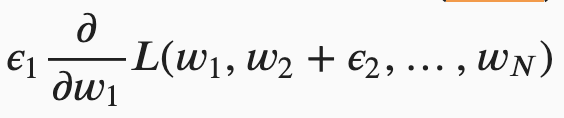The first part (i.e., ) equals to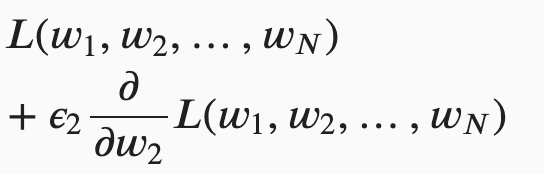 
;
The second part (i.e., ) equals to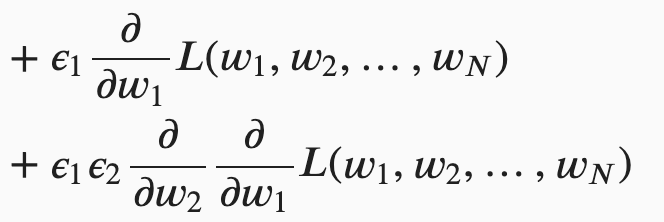 
.
@goldpiggy Thank you very much for your reply. Unfortunately it’s still not clear to me. I understand the first part, which basically comes from 18.3.6 again. But I’m just really stuck at the second part. I don’t seem to see the algebraic steps behind it, and am not familiar with rewriting terms containing partial derivatives (or functions containing multiple variables for that matter, using strictly function notation). I’m going to leave it be for the moment (have been obsessing about this for a while now), and return to it later. Hopefully I can understand it then. Perhaps you can point me in the direction of literature which explains the underlying logic of these equations in a bit more detail. Would be really helpful.
Maybe there is a part of ‖𝐯‖ missing in formula(18.4.10), where we use the dot product.
In the following explanation, they assume the magnitude of the direction, which is |v|, equals to 1. Then it can be discarded.