Can someone please help me with this part. I am not able to interpret from the code examples what the statement is trying to say
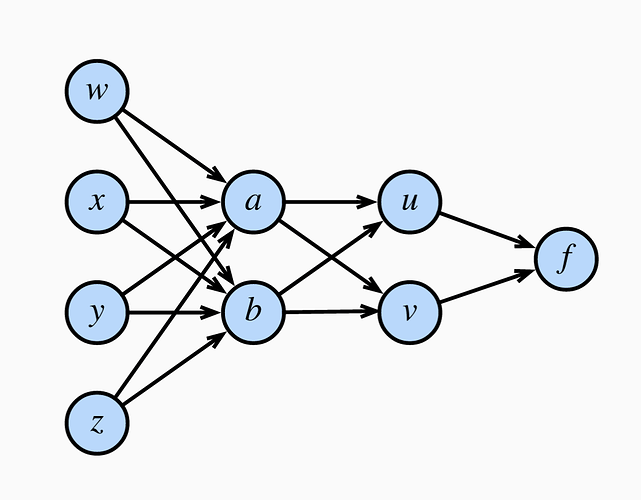
This requires understanding the chain rule using the graph
We want to compute df/dw, df/dx, df/dy, and df/dz, and the chain rule says that we do df/dw by considering all the paths from w to f, and multiplying/adding the derivative associated to each edge or single step (e.g. df/du or du/da or da/dx)
All these single step derivatives are computed first, let’s call this (as the book does) a “forward pass” or step 0, there is no getting around that.
Now paths from x to f (in order to compute df/dx) , such as , x ->a->u->f,
can be successively built up either
- forward from paths that start at x, x-a, x-a-u, x-a-u-f
- or backwards from paths that end at f: u-f, a-u-f, x-a-u-f
Both ways will work (also have to consider x-a-v-f, etc)
If we want to compute df/dw, we need to consider paths w ->f, and the point is that if we already did df/dx the backwards way, we can reuse the calculations we did: we can break up w-a-u-f as w-a and a-u-f, and the a-u-f we have seen (and stored df/da) when breaking the path x-a-u-f the backwards way via x-a and a–u-f.
By contrast, if we break up paths the forward way in computing df/dx, e.g. x-a, x-a-u, x-a-u-f, these partial paths all start with x, and so are no use for calculations involving (forward) paths that start at w! It is still possible to compute df/dw via w-a, w-a-u, w-a-u-f, etc (not going to list all) but you don’t get a chance to reuse previous calculations.