https://d2l.ai/chapter_attention-mechanisms-and-transformers/multihead-attention.html
Exercises2
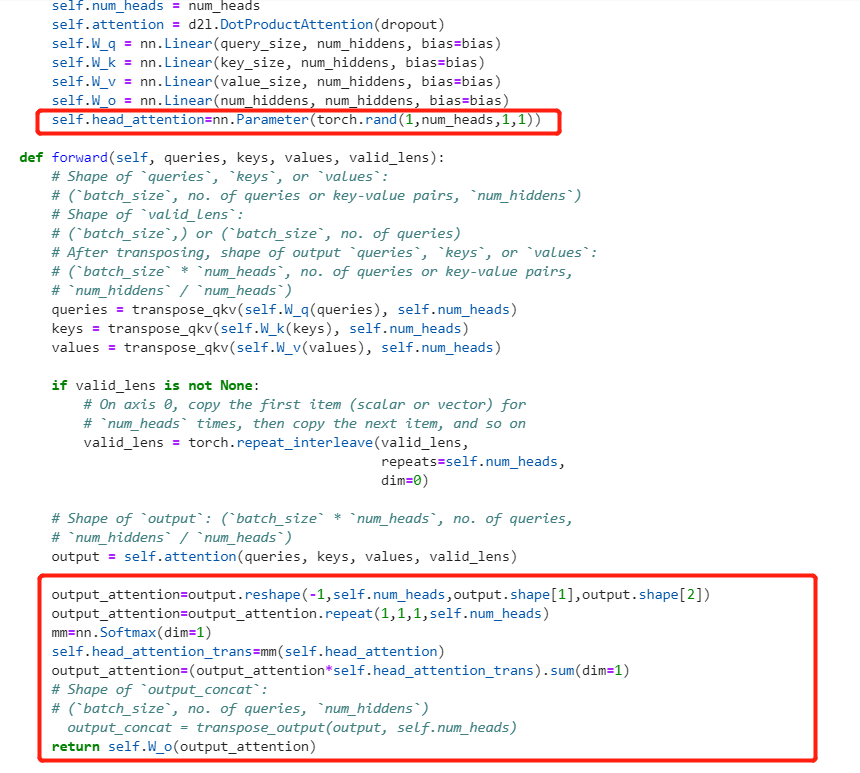
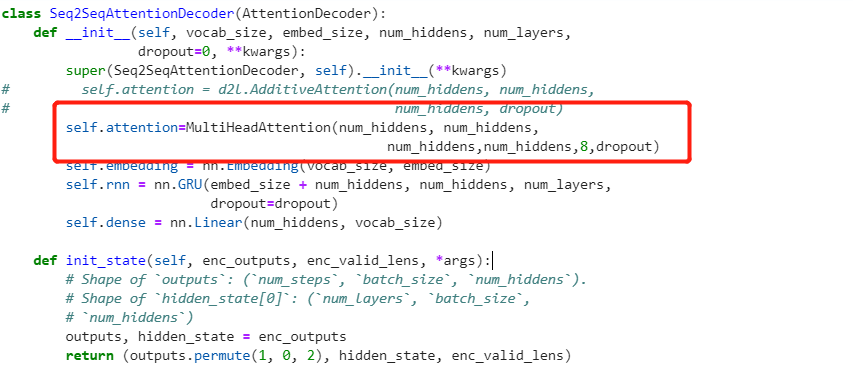
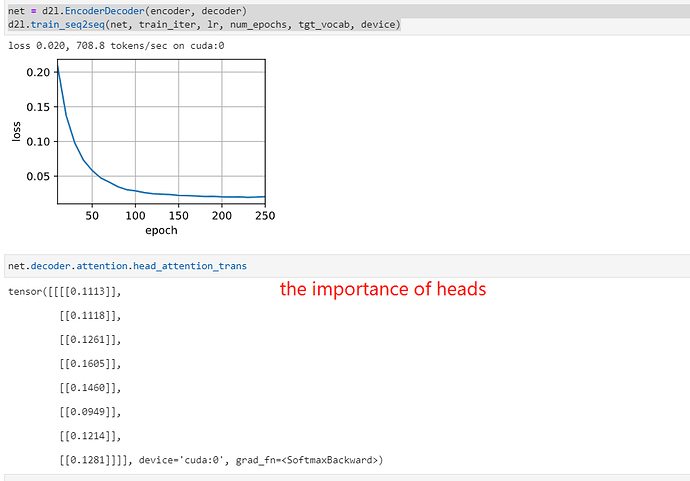
i make a experiments:
in multi_attention the output is [batch_size,num_heads,queries,num_hiddens/num_heads]
i want to add a softmax to the output to check the weights of the output .
the vectof of first vector is [batch_size,0,queries,num_hiddens/num_heads] ,repeate the last dim num_heads, so we can have a vector [batch_size,num_heads,queries,num_hiddens]. then use the softmax weight to measure the weight of the heads.
For torch implementation, multi-head attention says it will train “ℎ independently learned linear projections.” However, the implementation for MultiHeadAttention has fixed number of parameters. Anyone can explain why is it? I think it should have ℎ times more parameters than single head attention.
The last dimension of queries is num_hidden, but the input size of w_q is query_size. What if num_hidden is not equal to query_size?
in the implementation, there is a special setting:
![]()
and Po= num_hiddens.
so for each linear projection, the output dimension should be num_hiddens/h
in the code, it set the linear network to a bigger one, with shape as (query_size, num_hiddens), it means there will be h time of W parameters then a single linear net.
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
in the special implementation it sets query_size=k_size=v_size=num_hiddens, which can be found in the attention layer initialization:
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
这一章与其说是实现了多头注意力,不如说是实现了一个巨大的单头注意力,多个头实现并行那一段代码,的确不好理解,变来变去。
transpose_qkv-》transpose_output
莫非这就是transformer名字的来由?
Thank you for the reply! I can understand this is a special implementation for running efficiency, but it does make it very hard to understand what is actually happening in a general transformer.
Hi, zppet, thank you for sharing your understanding, however I still have some questions for this section.
We have “pqh=pkh=pvh=po In the following implementation, po is specified via the argument num_hiddens”, which indicates that qury_size * num_heads = key_size * num_heads = value_size * num_heads = num_hiddens. And we also have num_hiddens = query_size as you mentioned here:
However, this rises an ineuality considered that we define num_heads as 5 (in the following code block).
Could you please explain this point?
Hello,
In the comment of the forward method of MultiHeadAttention, shouldn’t the original queries (/keys/values) shape be (batch_size, no. of queries, query_size), so that when it get multiplied by self.W_q it returns shape (batch_size, no. of queries or key-value pairs, num_hiddens)?
#@save
class MultiHeadAttention(nn.Module):
...
def forward(self, queries, keys, values, valid_lens):
# Shape of `queries`, `keys`, or `values`:
# (`batch_size`, no. of queries or key-value pairs, `num_hiddens`) <------ HERE
# Shape of `valid_lens`:
# (`batch_size`,) or (`batch_size`, no. of queries)
# After transposing, shape of output `queries`, `keys`, or `values`:
# (`batch_size` * `num_heads`, no. of queries or key-value pairs,
# `num_hiddens` / `num_heads`)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
values = transpose_qkv(self.W_v(values), self.num_heads)
...
Thanks in advance.
谢谢大佬的解答,不看你的评论确实很容易忽略掉这个细节,导致看不懂代码
Exercise 1 :
add one line code this is right? d2l.show_heatmaps(attention.attention.attention_weights.reshape((batch_size, num_heads, num_queries, num_kvpairs)), xlabel='Keys', ylabel='Queries',figsize=(5, 5))
and this is the attention weight of each head ? 
W_q、W_k和W_v不应该是有h个吗,为什么类实现里面就写了一个
Hi, I suppose the multi-head is different from a big single-head,
though both are weighted-sum of transformed values,
for different head part of the transformed values will have different weights.
It is that only in computing the transformed q,k,v, due to some independence property of linear transform, we can seemingly write a big linear transform as a whole to enhance computation efficiency.
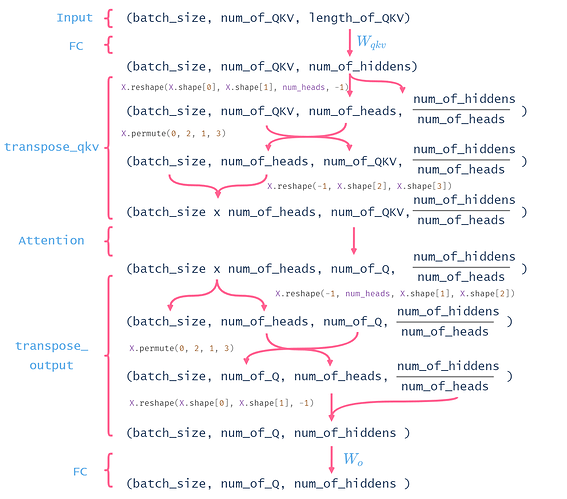
The code in this section is so confusing ![]() . I made this picure to help myself sort out how the shape of tensor change within multihead attention.
. I made this picure to help myself sort out how the shape of tensor change within multihead attention.
I agree that the reshaping is making things more confusing and what you gain in efficiency you lose in clarity. I manage to make another version using a for-loop this time to avoid the reshaping, I hope it’s correct and that it will help others to better understand the MultiHeadAttention.
class MultiHeadAttention(nn.Module):
def __init__(self, num_hiddens, num_heads, dropout, bias=False, **kwargs):
super().__init__()
# For simplicity we set p_o = num_hiddens
p_o = num_hiddens
# For simplicity we set p_q = p_k = p_v = p_o // num_heads
p_q = p_k = p_v = p_o // num_heads
self.num_heads = num_heads
self.attention = DotProductAttention(dropout)
self.W_q = nn.ModuleList([nn.LazyLinear(p_q, bias=bias) for _ in range(self.num_heads)])
self.W_k = nn.ModuleList([nn.LazyLinear(p_k, bias=bias) for _ in range(self.num_heads)])
self.W_v = nn.ModuleList([nn.LazyLinear(p_v, bias=bias) for _ in range(self.num_heads)])
self.W_o = nn.LazyLinear(p_o, bias=bias)
def forward(self, queries, keys, values, valid_lens):
heads = []
for i in range(self.num_heads):
qs = self.W_q[i](queries) # (batch_size, num_queries, num_hiddens) -> (batch_size, num_queries, num_hiddens // num_heads)
ks = self.W_k[i](keys) # (batch_size, num_kvpairs, num_hiddens) -> (batch_size, num_kvpairs, num_hiddens // num_heads)
vs = self.W_v[i](values) # (batch_size, num_kvpairs, num_hiddens) -> (batch_size, num_kvpairs, num_hiddens // num_heads)
head = self.attention(qs, ks, vs, valid_lens) # (batch_size, num_queries, num_hiddens // num_heads)
heads.append(head)
concat_heads = torch.concat(heads, dim=2) # (batch_size, num_queries, num_hiddens)
outputs = self.W_o(concat_heads)
return outputs
You seem to have run out of letters. Letter h now means everything.

The original paper show that (11.5.2) is wrong.
what are p_k, p_v, p_q?