For exercise 4 of this section, what is meant by “long range convolution”? and is this common terminology?
Thank you 
Hey @smizerex, great catch! “long range” means a large size of convolutional filter. Does it make sense?
Can someone explain to me how does a 1x1 Conv layer reduces the number of channels?
Isn’t the number of output channels a manual specification?
The middle two paths perform a 1x1 convolution on the input to reducethe number of channels, reducing the modelʼs complexity. The fourth path uses a 3x3 maximum pooling layer, followed by a 1x1 convolutional layer to change the number of channels
(as quoted from the text)
My understanding is that kernel size does not reduce the number of channels. What am I missing?
As far I understand, 1x1 conv, when applied with default parameters (padding, strides)=(0,1) change the number of output channels only. This number of output channels may be greater equal or lesser then input channel.
In such conditions, the 1x1 transformation leads to following tensor-shape transformation :
Ci x H x W → Co x H x W
where
- Ci is the number of input channels
- Co is the number of output channels
- H and W are 2D size Hight and Weight
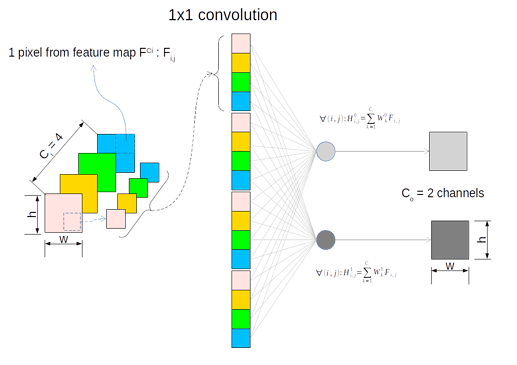
May be the following scheme will help. This is a 1x1 conv. model transforming 4 input channels into 2 input channels.
Thanks for the visualisation.
So, here the Co is manually specified right? That was my doubt actually.
General practice is to reduce the number of channels right?
Also, what happens to the complexity of the model? Does it reduce?
(I understand less channels = less computation, but by doing this, are we making the model more abstract?)
So, here the Co is manually specified right? That was my doubt actually.
Yes, Co, number of output channels, is specified manually. E.g, this is a parameter for
nn.conv2Dgluon API.General practice is to reduce the number of channels right?
On my sense, not necessarily. For computer vision, practice is, layer after layer, to increase the number of channels while reducing images spatials dimensions. This lead to more abstracts objects when calculation progresses through the convolutional layers.
Also, what happens to the complexity of the model? Does it reduce?
On my understanding, this makes sense that model complexity reduces along with calculation progression through the neural layers. Data is then encoded more and more efficiently then, less bit of informations are required to describe data then, as you mentioned, complexity decreases. This is a direct consequence of entropy reduction that is targeted through loss function in case of classification.
But, globally, taking into account all parameters into the (deep) neural model (those parameters used for tensor calculation into layers units) it seems the model complexity increases with the complexity of the problem to be processed.
great! ‘entropy reduction’ do you mean to enhance the differences of classifications?
Yes, if less bit are required to encode information, this mean noise is reduced and then, as a consequence, “confusion” is reduced leading to better model performance for classification.