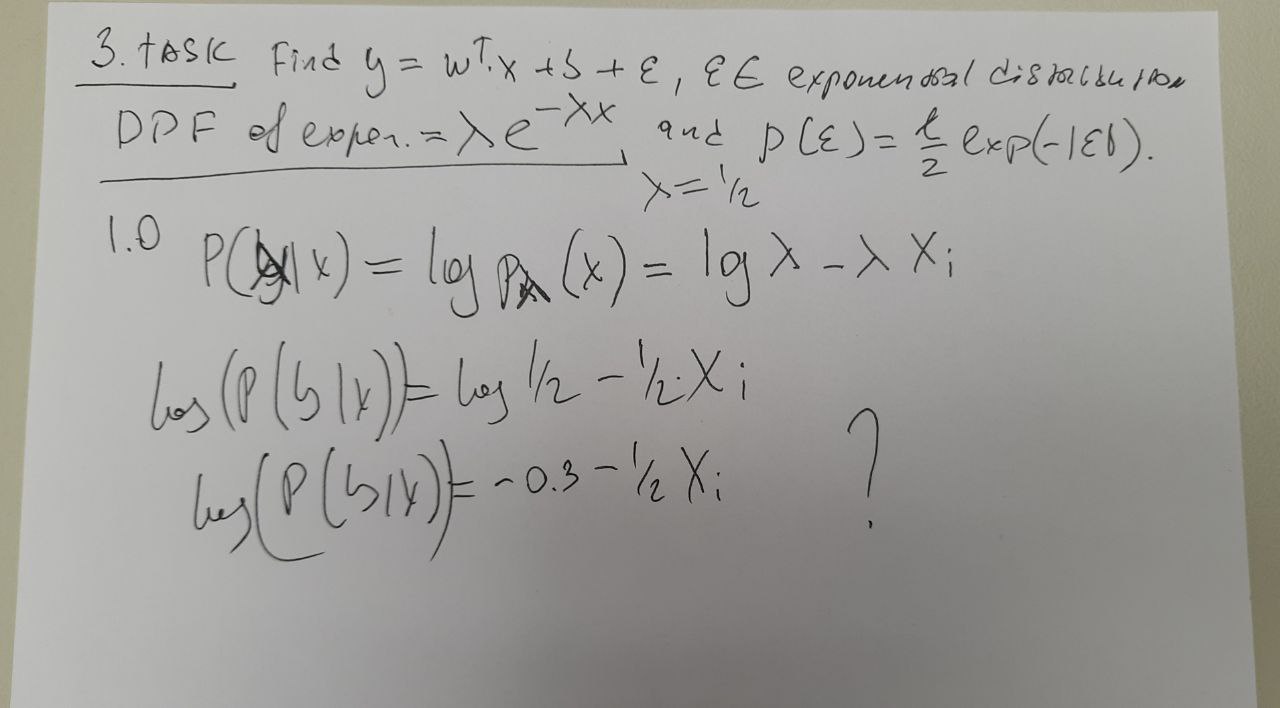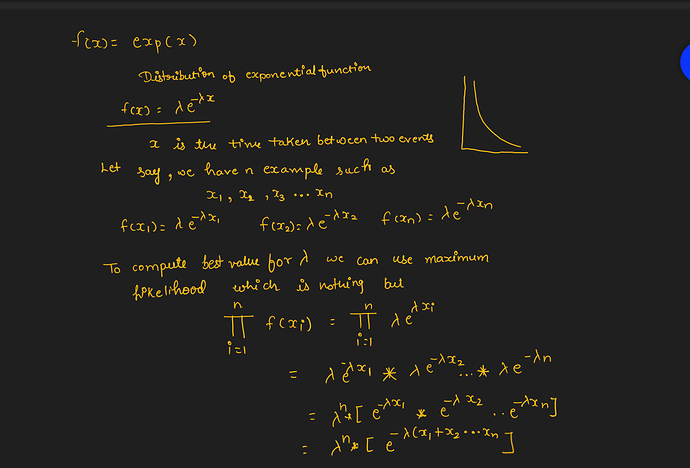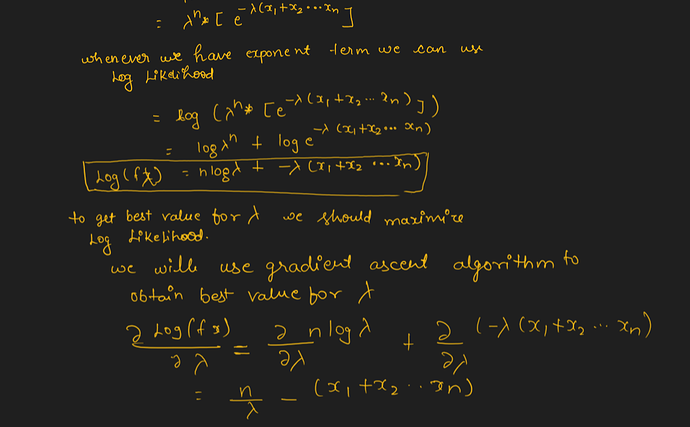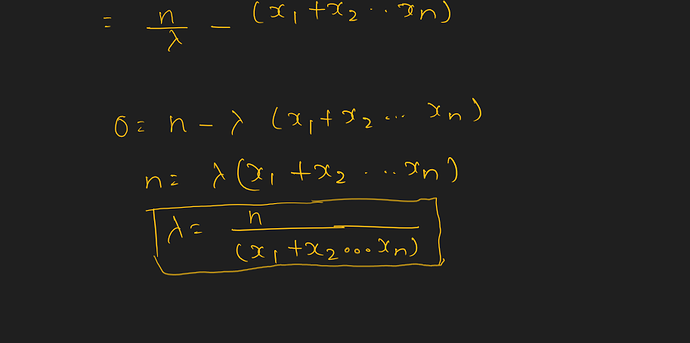Linear Regression

[mli]

https://d2l.ai/chapter_linear-regression/linear-regression.html

[meetashok]

After training for some predetermined number of iterations (or until some other stopping criteria are met), we record the estimated model parameters, denoted 𝐰̂ ,𝑏̂ w^,b^. Note that even if our function is truly linear and noiseless, these parameters will not be the exact minimizers of the loss because, although the algorithm converges slowly towards the minimizers it cannot achieve it exactly in a finite number of steps.

I have a question about the part in bold. If we choose a large learning rate, then the algorithm can overshoot the parameter values for which loss function is minimized. So, that tells me that we should be able to find w, b that minimize the loss exactly. What could I be missing?

[meetashok]

For Q1 from the exercises, the solution for b would be the sample mean of the data. How does it relate to the normal distribution - could someone help?

Assume that we have some data 𝑥1,…,𝑥𝑛∈ℝx1,…,xn∈R. Our goal is to find a constant 𝑏b such that ∑𝑖(𝑥𝑖−𝑏)2∑i(xi−b)2 is minimized.

1. Find a analytic solution for the optimal value of 𝑏b.
2. How does this problem and its solution relate to the normal distribution?

[osamaGkhafagy]

I believe the optimal value of b is equal to the mean of the whole dataset which represents the Mean of a normal distribution. This makes (X_i - b) is the same as the exponent of e (X_i - mu)

[sushmit86]

In question 3 should the distribution be laplace or double exponential?

[mxnetuser]

I found that the code can’t be run in COLAB because mxnet can’t be imported.

[Felipe_Chinen]

I don’t know if I’m right, but intuitively, the normal distribution shows what are the most common values.

sum i to n of (xi-b)^2 = sum xi^2 + sum b^2 + sum 2*(xi-b)

So, b = mean of x should cancel or get values close to zero to the majority of the function.

[VolodymyrGavrysh]

1.Assume that we have some data x1 , x2 … , xn ∈ R. Our goal is to find a constant b such that
∑i (x i − b)^2 is minimized.

1. Find a analytic solution for the optimal value of b.
2. How does this problem and its solution relate to the normal distribution?

My answer

let have n = 2, than
x1^2 + x2^2 = 2*b (x1 + x2 - b) => find a min b
comes to
(x1 + x2) / 2 = b

To have min b, you need it equal to mean of X.

for the second quesiotn

∑(x i − b)^2 is exactly MSE if b becomes mean(xi) for minimizing general error. Assuming that errors are distributed normally, b in this case become mu of that distribution (variance is not counted)

[VolodymyrGavrysh]

For the second question

[VolodymyrGavrysh]

Task 3 (partly, not sure if it is correct at all)

[Ismail_Moussaoui]

i don’t understand the solution of the first question , explanation ?

[ning_ke]

when i use the notebooks from https://github.com/d2l-ai/d2l-en(by git clone),every notebook has code segment which you can see by picture.when i run code ,there is a error ,can you tell me usefulness of code segment

[Anish_Yadav]

Hello,

I tried to solve the question. Kindly check below screenshots.

[Anish_Yadav]

@Anish_Yadav Continue

[Anish_Yadav]

@Anish_Yadav Continue