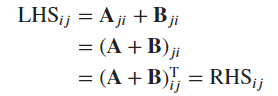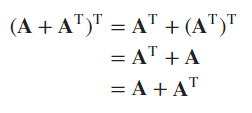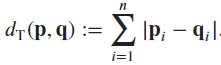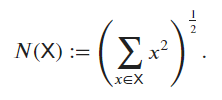Exercise 1
import torch
A = torch.arange(6, dtype=torch.float64).reshape(2, 3)
(A.T).T == A
tensor([[True, True, True],
[True, True, True]])
Exercise 2
B = A.clone()
A.T + B.T == (A + B).T
tensor([[True, True],
[True, True],
[True, True]])
Exercise 3
M = torch.arange(9, dtype=torch.float64).reshape(3, 3)
M + M.T == (M + M.T).T
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
Exercise 4
The tensor X has the shape (2, 3, 4), meaning it has 2 elements in the first dimension, each being a tensor of shape (3, 4). Therefore, the output of len(X) is 2, as this function returns the size of the first dimension of a tensor.
X = torch.arange(24).reshape(2, 3, 4)
len(X)
2
Exercise 5
Yes, len(X) will always correspond to the length of the first axis (axis 0).
Exercise 6
try:
A / A.sum(axis=1)
except Exception as error:
print(A.shape, A.sum(axis=1).shape, error, sep="\n")
torch.Size([2, 3])
torch.Size([2])
The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 1
Notice that A and A.sum(axis=1) have different dimensions, so the operation does not occur. The error, therefore, informs that the division requires the sum vector to be resized to match the dimensions of the original matrix. Like this:
A / A.sum(axis=1, keepdim=True)
tensor([[0.0000, 0.3333, 0.6667],
[0.2500, 0.3333, 0.4167]], dtype=torch.float64)
Exercise 7
Source:
Taxicab geometry and
map of Manhattan Center.
Exercise 8
X = torch.arange(24).reshape(2, 3, 4)
X,X.sum(axis=0), X.sum(axis=1), X.sum(axis=2)
(tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]]),
tensor([[12, 14, 16, 18],
[20, 22, 24, 26],
[28, 30, 32, 34]]),
tensor([[12, 15, 18, 21],
[48, 51, 54, 57]]),
tensor([[ 6, 22, 38],
[54, 70, 86]]))
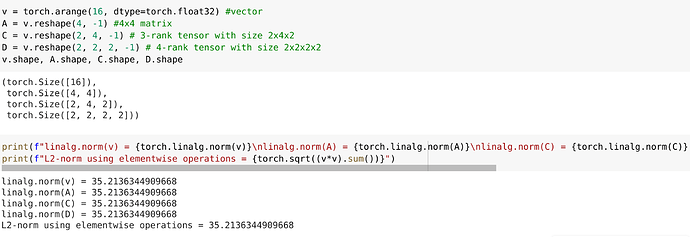
Exercise 9
X = torch.arange(24, dtype=torch.float64).reshape(2, 3, 4)
torch.linalg.norm(X)
tensor(65.7571, dtype=torch.float64)
torch.linalg.norm() computes the Frobenius norm for matrices (2D tensors) and the L2 norm for tensors with more than two dimensions. Thus, the previous result represents the magnitude of the vector in a high-dimensional space formed by flattening the tensor X. Applying this function “forcefully”:
def l2(tensor):
return torch.sqrt(torch.sum(tensor ** 2))
l2(X)
tensor(65.7571, dtype=torch.float64)
Exercise 10
import psutil
import time
def memory(X, Y):
start = time.time()
torch.mm(X, Y)
memory = psutil.virtual_memory()
print(f"Total system memory: {memory.total / (1024 ** 3):.2f} GB")
print(f"Memory used: {memory.used / (1024 ** 3):.2f} GB")
print(f"Available memory: {memory.available / (1024 ** 3):.2f} GB")
print(f"CPU usage: {psutil.cpu_percent():.2f}%")
elapsed = time.time() - start
print(f"Elapsed time: {elapsed:.2f} seconds\n")
torch.manual_seed(42)
A = torch.randn(2 ** 10, 2 ** 16, dtype=torch.float64)
B = torch.randn(2 ** 16, 2 ** 5, dtype=torch.float64)
C = torch.randn(2 ** 5, 2 ** 14, dtype=torch.float64)
memory(torch.mm(A, B), C)
memory(A, torch.mm(B, C))
Total system memory: 19.23 GB
Memory used: 2.82 GB
Available memory: 15.72 GB
CPU usage: 21.10%
Elapsed time: 0.05 seconds
Total system memory: 19.23 GB
Memory used: 10.82 GB
Available memory: 7.75 GB
CPU usage: 70.70%
Elapsed time: 27.60 seconds
Exercise 11
I believe there is a typographical error in this question because the operation torch(A, B.T) is not possible due to dimension incompatibility. In this case, I did C = C.T (which I think is what the authors actually intended).
torch.manual_seed(42)
C = torch.randn(2 ** 5, 2 ** 16, dtype=torch.float64)
memory(A, B)
memory(A, C.T)
C = C.T
memory(A, C)
Total system memory: 19.23 GB
Memory used: 3.26 GB
Available memory: 15.22 GB
CPU usage: 12.00%
Elapsed time: 0.07 seconds
Total system memory: 19.23 GB
Memory used: 3.28 GB
Available memory: 15.22 GB
CPU usage: 15.00%
Elapsed time: 0.06 seconds
Total system memory: 19.23 GB
Memory used: 3.27 GB
Available memory: 15.22 GB
CPU usage: 9.50%
Elapsed time: 0.07 seconds
-
Theoretically, the operations torch.mm(A, B) andtorch.mm(A, C.T) should have similar performance in terms of computational complexity, but differ in memory access due to the data orientation of C.T. It was expected that transposition would negatively affect efficiency due to non-sequential memory access. However, the time difference between torch.mm(A, B) and torch.mm(A, C.T) is minimal. Perhaps the internal optimization of PyTorch for transpose operations is quite effective, minimizing the theoretically negative impact of memory transposition.
-
Pre-transposing Cand performing the multiplication with A shows a runtime comparable to torch.mm(A, B), with slightly reduced CPU usage. The reduction in CPU usage may be due to the elimination of the need for dynamic transposition during multiplication, indicating that pre-processing C might be beneficial from the perspective of reducing CPU load, despite not significantly impacting runtime.
Exercise 12
torch.manual_seed(42)
A = torch.randn(100, 200, dtype=torch.float64)
B = torch.randn(100, 200, dtype=torch.float64)
C = torch.randn(100, 200, dtype=torch.float64)
torch.stack([A,B,C]).shape, torch.stack([A,B,C])[1] == B
(torch.Size([3, 100, 200]),
tensor([[True, True, True, ..., True, True, True],
[True, True, True, ..., True, True, True],
[True, True, True, ..., True, True, True],
...,
[True, True, True, ..., True, True, True],
[True, True, True, ..., True, True, True],
[True, True, True, ..., True, True, True]]))
, because the difference between them is not so obvious, so is there anybody who have any other way to do this exercise?
and forced to restarted…
. But I believe we travel along streets/roads that lead us to our destination. We can’t travel diagonally since there will be things like houses and other buildings/parks/private properties getting in the way 
is divided by the summation of all elements in the row where 
to 
along a trajectory composed of only horizontal and vertical lines.
.
, the 
and 
is defined as
