Geometry and Linear Algebraic Operations

English Version pytorch
1

https://d2l.ai/chapter_appendix-mathematics-for-deep-learning/geometry-linear-algebraic-ops.html

2

The classifier used in the text seems rather unnatural. A more natural way is to flatten the images, normalize them, then take the dot product as discussed in the text as a measure of similarity. The predicted label is the label of the average image that is more similar to the test image, hence the argmax.

# normalize matrices using broadcasting
W = torch.stack([ave_0.flatten().t(), ave_1.flatten().t()], dim=1)
W = W / torch.norm(W, dim=0).reshape(1, -1)
X_test = X_test.reshape(-1, 784)
X_test = X_test / torch.norm(X_test, dim=1).reshape(-1, 1)

# predict and evaluate
y_pred = torch.argmax(X_test @ W, dim=1)
print((y_test == y_pred).type(torch.float).mean())

This obtains an accuracy of ~0.95. :grinning:

4 Likes
3

What’s the interpretation of A^4 in exercise 7?

4

I’ve typed up solutions to the exercises in this chapter here (see bottom of the notebook). I’m still seeking guidance on exercise 7.

Any help will be greatly appreciated!

5

Hey, maybe a little late here; but as far as I understand it, A^4 means a matrix with 4 dimensions.

6

Based on this section, I think A^4 means A * A * A * A, that is, matrix A multiplied 4 times by itself. It’s the power operator (A to the power of 4) for matrices, if I’m not mistaken.

7

In Section 18.1.3. Hyperplanes, it says - “The set of all points where this is true is a line at right angles to the vector w”. Which condition is “this” referring to here? Is it referring to all vectors (or rather, points here) whose projection is equal to 1/||w||?

8

# Accuracy\n torch.mean(predictions.type(y_test.dtype) == y_test, dtype=torch.float64)

Hi, I think the way to calculate the accuracy is not right here, since the predictions.type(y_test.dtype)==y_test will return a tensor which only contain the Boolean values. It can not be calculated by the torch.mean() function. So I think the right format should be:

torch.mean((predictions.type(y_test.dtype) == y_test).float(), dtype=torch.float64)

In this way the result is exactly the same.

9

Hi @Tate_Zenith,

Yes, the current implementation will raise a runtime error with the latest version of torch==1.10.2. This behaviour was fine if you try to run with torch==1.8.1.

I’ll send a fix to support the latest version. We’re working on making the master branch support the latest versions of all the frameworks.

1 Like
10

That’s sounds great, thanks!

11

Section 18.1.6:

… C has rank two since, for instance, the first two columns are linearly independent, however any of the four collections of three columns are dependent.

Questions/doubts:

  • Which four collections of three columns? There are 5C3=10 collections of 3 columns each that can be formed from the 5 columns. So, which 4 out of the 10 are being discussed here?
  • Perhaps, it can be made clearer by giving the proof of linear dependence of one of the collections.
12

@ToddMorrill
For exercise7, this is what I think the solution is:
PS. this solution concern A^4 as a matrix multiplication and not element wise multiplication.

D = A^4 = A^2.A^2 = B^2
tr(D) = {sum, i} d_ii
dii = {sum, j} b_ij*b_ji
bij = {sum, k} a_ik*a_kj
dii = {sum, j}({sum, k}a_ik*a_kj)*({sum, l}a_jl*a_li)
dii = {sum, j}{sum, k}{sum, l}a_ik*a_kj*a_jl*a_li
tr(D) = {sum, i}{sum, j}{sum, k}{sum, l}a_ik*a_kj*a_jl*a_li 
tr(A^4) = torch.einsum('ik,kj,jl,li', A, A, A, A)

I verified this answer with random matrices and it worked

size = 4
A = torch.randint(1, 100, (size, size))
tr_A_4 = torch.trace(torch.matmul(torch.matmul(A, A), torch.matmul(A, A)))
tr_A_4_einsum = torch.einsum('ik, kj, jl, li', A, A, A, A)
assert  tr_A_4 == tr_A_4_einsum
14

hope this can help you out:
torch.einsum(“ij,jk,kl,lm → im”, A,A,A,A).trace()

15

I don’t really understand the Tensors and Common Linear Algebra Operations subsection. The sum at 22.1.32 is a bit confusing.

16

Ex1.

  • Using the function angle(), we compute
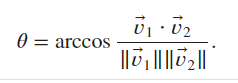
    image 
def angle(x, y):
    """
    Computes the angle between two vectors.
    """
    return torch.acos(x.dot(y) / (torch.linalg.norm(x) * torch.linalg.norm(y)))

rad = angle(
    torch.tensor([1, 0, -1, 2], dtype=torch.float32),
    torch.tensor([3, 1, 0,  1], dtype=torch.float32)
)
rad, rad / 3.14 * 180

Output (in rad and degree, respectively):

(tensor(0.9078), tensor(52.0412))

Ex2.

  • True. We can verify straightforwardly by definition.
M1 = torch.tensor([[1, 2], [0, 1]])
M2 = torch.tensor([[1, -2], [0, 1]])
M1 @ M2, M2 @ M1

Output:

(tensor([[1, 0],
         [0, 1]]),
 tensor([[1, 0],
         [0, 1]]))

Ex3.

  • The determinant is the scaling factor of the transfomred area. We compute the determinant of the transform matrix:
torch.det(torch.tensor([[2, 3], [1, 2]], dtype=torch.float32))

Output:

tensor(1.)
  • Since the determinant is 1, the area is left unchanged as 100.

Ex4.

  • Linear independence is equivalent to a non-zero determinant.
    • Below shows that only the first set of vectors is linearly independent.
is_linear_indep = lambda X: bool(torch.det(X))
X1 = torch.tensor([[1, 2, 3], [0, 1, 1], [-1, -1, 1]], dtype=torch.float32)
X2 = torch.tensor([[3, 1, 0], [1, 1, 0], [1, 1, 0]], dtype=torch.float32)
X3 = torch.tensor([[1, 0, 1], [1, 1, 0], [0, -1, 1]], dtype=torch.float32)
is_linear_indep(X1), is_linear_indep(X2), is_linear_indep(X3)

Output:

(True, False, False)

Ex5.

  • It is true. By definition,
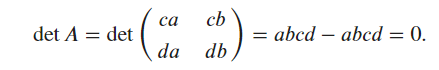
    image

Ex6.

  • We take the dot product,
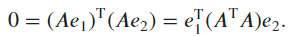
    image
    Denoting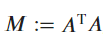 image, one has the condition for orthogonality which reads
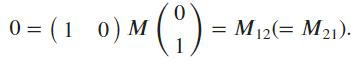
    image

Ex7.

  • We hierarchically “expand” the summation according to the definition of matrix multiplication:
    image

    • The corresponding Einstein summation notation should be ij, jk, kl, li ->, where an empty string is used to represent a scalar.
# Check our result
torch.manual_seed(706)
A = torch.randn(3, 3)
einsum = torch.einsum("ij, jk, kl, li ->" , A, A, A, A)
manual = torch.trace(A @ A @ A @ A)
einsum.item(), manual.item()

Output:

(141.1223907470703, 141.12237548828125)
17

The visualization at the start of 22.1.3. Hyperplanes in the image “Fig. 22.1.5 Recalling trigonometry, we see the formula ‖𝑣‖cos⁡(𝜃) is the length of the projection of the vector 𝑣 onto the direction of 𝑤” is not accurately representing the 𝑦=1−2𝑥 equation. The line should intersect the y-axis at (0, 1), not at (0, 2) as shown.