@peng look: " so the above loss near 0" the generator tries to maximize this cost -log(1-d(g(z))), and the max value for that is not zero! it is infinite. you can easily plot -log(1-d(g(z))) at here: https://www.desmos.com/calculator
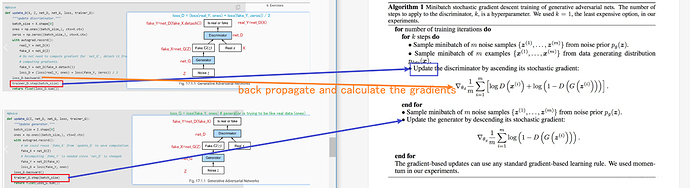
The snippet in function update_D
# Do not need to compute gradient for `net_G`, detach it from
# computing gradients.
fake_Y = net_D(fake_X.detach())
loss_D = (loss(real_Y, ones.reshape(real_Y.shape)) +
loss(fake_Y, zeros.reshape(fake_Y.shape))) / 2
loss_D.backward()
Why not compute the gradient for net_G? As what we can see, fake_Y = net_D(net_G(Z)), since fake_Y is a part of the computation of loss_D, on which we call the backward(). So I can’t figure out the reason to call detach on net_G(Z), I mean, the variable fake_X.
Here’s my trial to not to detach fake_X:
For comparison, the second pic is the “detach” ver, whose code is the same as the tutorial:
(for the sake of the restriction for new user in this website, the second pic is posted below)
For comparison, the second pic is the “detach” ver, whose code is the same as the tutorial:
@goldpiggy thanks in advance!
Yes, this sentence is so confusing to me.
Generally we calculate gradients to update network parameters later. But in the function update_D, we just want to update the parameters of network D. So the gradients of the parameters in network G are not needed. Since keeping track of the gradients is computationally expensive, it is better to detach fake_X first.