https://d2l.ai/chapter_generative-adversarial-networks/gan.html
Greetings,
I really appreciated the simplicity of this GAN demonstration. Is there a way to extract the contents of net_G and compare them with A and b that were defined at the start, to show that the generator has effectively deduced the parameters used to set up the “real” data? I tried print(net_G[0]), but it just says Dense(2 -> 2, linear). How do I get it to show the actual numbers? I know that for large layers and convnets and so forth, the numbers get enormous, and not easy to simply look at and interpret, but I would think that this example would allow one to close the loop and show that the results of the training actually do match the inputs. The scatter plot shows that, graphically, but I’d love to see the numbers, too.
Thank you,
Don
Quick update. I figured out print(net_G[0].weight.data()) and print(net_G[0].bias.data()), but while the bias data looked relatively close to b, the weights looked nothing like A, so I think I am still not understanding something. Thanks for any insight you can provide.
Yours,
Don
Hi @Donald_Smith, great question! The bias are closed because the “Real” data was generated following a Normal distribution, which lead to a zero intercept at y axis.
However, as the weights of net_G apply to the noise Z (rather than like the biases of net_G apply to “1”), so we should expect net_G(Z) is close to the “data”.
Let me know if that makes sense to you!
Almost. I feel like I’m close, but not quite there.
As presented, I can see the graph with the blue and orange dots on them, and see intuitively that the distribution of orange dots is “like” the blue ones (and the animation wonderfully shows how it becomes “more like” with the training). I would like to take that visual intuition and be more quantitative about it. If I am reading this correctly, the blue dots are created by taking 2000 points from a normal gaussian distribution, treating them as X/Y coordinates, and then transforming them through a matrix multiplication and a vector translation to get the stretch and spread in the plot (although only 100 points of the 1000 are plotted).
The train function then generates 100 pairs of normal gaussian numbers (Z) and passes them to net_G, to make “fake_X”, which is then plotted as orange dots. If the orange dots match the blue dots, then it should be the same transformation (or at least not different).
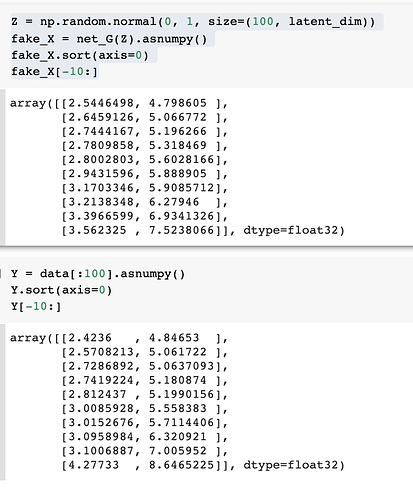
What I would like to do, and I have very little experience with mxnet, is extract exactly what numbers net_G is using to go from Z to fake_X, so I can compare, quantitatively, those numbers with A and b that were used back to take “X” to “data” at the beginning. Clearly, net_G[0].weights.data() are not those numbers, so, how do I get those numbers?
Or am I still not understanding what it’s doing?  In short, I would like to know exactly what the line fake_X = net_G(Z).asnumpy() is doing.
In short, I would like to know exactly what the line fake_X = net_G(Z).asnumpy() is doing.
Thanks for your help!
Don
Hi @Donald_Smith, we are not learning A but learning the data. (Maybe we should use another representation like “fake_data” rather than “fake_X”.)
As a result, you can compare the following:
Oh. Oh! I think I get it now. net_G is not applying the same transformation (* 2x2 matrix + 2x1 vector), it’s figuring out some kind of transformation that makes fake_X look “the most like” data. Is that right? I’ve done NN code to try to figure out linear fit parameters (total overkill, I know – it was an illustration to compare how a NN would do it compared with a least squares matrix transposition). I was interpreting this as trying to use loss minimization to drive the transformation parameters to get as close as possible to the original parameters. I got sidetracked by the fact that the first layer was a 2x2 matrix, so I thought by training the weights, it was figuring out a best match for A. But now, if I understand it better now, it’s doing a different transformation from Z to fake_X, and trying to minimize the difference between “data” and fake_X.
Thanks – I’m trying to understand what’s going on inside the “black box”. Am I closer? 
Yours,
Don
That’s correct! It’s always fascinating to go through this thought process, while it is hard to unravel the blackbox if you have a model with billions parameters ![]()
PyTorch version: http://preview.d2l.ai/d2l-en/master/chapter_generative-adversarial-networks/gan.html
Exercises
An equilibrium exists when the generator catch up with all real data.
Does time.stop() mean that only first epoch time?
Yes, it times for one epoch.
why the loss of discriminator become bigger and bigger?
Hi @guanguanboy, great question. Here are two tips:
-
It’s common to see the generator loss was much higher than the discriminator loss. Try a double or triple weights update of the generator for each discriminator weights update.
-
When the loss explodes, try a lower learning rate and restart the training from scratch.
At first the generator is really poor and the discriminator’s job is really easy, so the loss of discriminator is low. But it does not mean that the discriminator is good at distinguishing fake data from real data. After some epochs, the generator becomes expert at generating fake data, so discriminator’s job becomes harder and harder. Hence the loss function increases. But it does not mean that the discriminator is not getting better at distinguishing fake from real. It means that its job is getting really hard.
@goldpiggy Good advise. Thank you.It’s my first comment on D2L community and you’re the first expert to response.
def update_G(Z, net_D, net_G, loss, trainer_G):
“”“Update generator.”""
batch_size = Z.shape[0]
ones = np.ones((batch_size,), ctx=Z.ctx)
with autograd.record():
# We could reuse fake_X from update_D to save computation
fake_X = net_G(Z)
# Recomputing fake_Y is needed since net_D is changed
fake_Y = net_D(fake_X)
loss_G = loss(fake_Y, ones)
loss_G.backward()
trainer_G.step(batch_size)
return float(loss_G.sum())
Why we are computing the gradients for the net_D parameters ??
Hi @uniq, could you elaborate your question? In this function, we only calculate the gradient of 𝐺, i.e., for a given discriminator 𝐷, we update the parameters of the generator 𝐺.