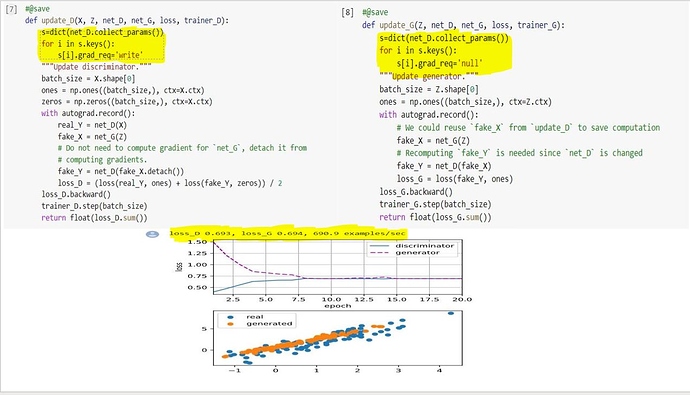
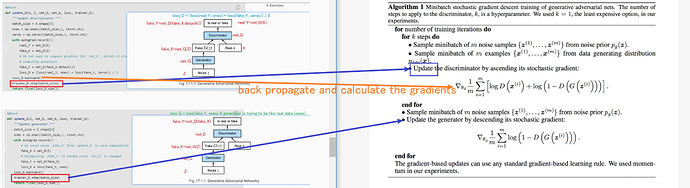
There is no expression involving gradients of the discriminator network. Then why we need to calculate it ?
Thanks in advance
…
I can’t understand what you are drawing…
Is it net_D?
Sorry about my handwriting. If you write the expression for d(loss_G) / d(G) , will you find anywhere in the chain rule the expression involving gradients of D ? This is my question…Hope I am clear…If there is no expression involving gradients of D, then why we need to compute it? We can set the grad_req to be null right ?
Thanks in advance
I don’t think we still need to compute the gradients of the Discriminator network. Can you show me the chain rule expression from loss_G to the net_G involving anything with the gradients of net_D ?
This is what I am trying to convey. I still get the same loss configuration If I set the discriminator network’s parameters gradient_requirement to be null in the update_G function. Correct me If I am wrong. If the discriminator network were a large neural network , then computing the gradients will be a costly operation.
I’m not sure about my opinion.
But my thoughts are that we don’t update gradient for net_D in the update_G function, but only computing the gradient of net_D.
See the description for ‘null’. It says the gradient arrays will not be allocated. Therefore , how will the gradients will be calculated and where it will be stored ?
" If the generator does a perfect job, then D(x′)≈1D(x′)≈1 so the above loss near 0, which results the gradients are too small to make a good progress for the discriminator. So commonly we minimize the following loss:"
Don’t you think this will lead to a large error? You can simply plot it.

I guess this final expression is what the loss_G.backward() calculates, which should include net_G and net_D in the code because the gradient is calculated using the weights in net_D and net_G.
Hi, very impressive discussion about the “black box”. I wonder if any progress for GAN learning the exact matrix A and b just using the “real data”. Or maybe the NN just care about the result. That is interesting because we could have various A and b to make the data looks the “same”, howerve, they are actually different. @goldpiggy @Donald_Smith
@peng look: " so the above loss near 0" the generator tries to maximize this cost -log(1-d(g(z))), and the max value for that is not zero! it is infinite. you can easily plot -log(1-d(g(z))) at here: https://www.desmos.com/calculator
The snippet in function update_D
# Do not need to compute gradient for `net_G`, detach it from
# computing gradients.
fake_Y = net_D(fake_X.detach())
loss_D = (loss(real_Y, ones.reshape(real_Y.shape)) +
loss(fake_Y, zeros.reshape(fake_Y.shape))) / 2
loss_D.backward()
Why not compute the gradient for net_G? As what we can see, fake_Y = net_D(net_G(Z)), since fake_Y is a part of the computation of loss_D, on which we call the backward(). So I can’t figure out the reason to call detach on net_G(Z), I mean, the variable fake_X.
Here’s my trial to not to detach fake_X:
For comparison, the second pic is the “detach” ver, whose code is the same as the tutorial:
(for the sake of the restriction for new user in this website, the second pic is posted below)
For comparison, the second pic is the “detach” ver, whose code is the same as the tutorial:
@goldpiggy thanks in advance!
Yes, this sentence is so confusing to me.
Generally we calculate gradients to update network parameters later. But in the function update_D, we just want to update the parameters of network D. So the gradients of the parameters in network G are not needed. Since keeping track of the gradients is computationally expensive, it is better to detach fake_X first.