https://d2l.ai/chapter_linear-regression/generalization.html
Some questions regarding the validation set:
In practical applications, the picture gets muddier. While ideally we would only touch the test data once, to assess the very best model or to compare a small number of models to each other, real-world test data is seldom discarded after just one use. We can seldom afford a new test set for each round of experiments.
Isn’t the validation set used to assess the best model or compare the models to each other? Here’s it is mentioned that the test set is used for this purpose. Is this a typo?
Therefore, the accuracy reported in each experiment is really the validation accuracy and not a true test set accuracy. The good news is that we do not need too much data in the validation set. The uncertainty in our estimates can be shown to be of the order of O(n^-0.5)
Can someone please share any resource on how the complexity was derived to be O(n^-0.5)?
Thanks!
In 4.4.4.2. Training and Testing Model
metric = d2l.Accumulator(2) # sum_loss, num_examples
I didn’t understand what Accumulator really do?
So I tried to read
http://d2l.ai/_modules/d2l/torch.html#Accumulator.
In def add,
self.data = [a+float(b) for a, b in zip(self.data, args)]
And I tried to contrast it with the first answer in
https://stackoverflow.com/questions/534855/subtracting-2-lists-in-python.
But, I am still curious about the necessity of float() and what args represents.
Why metric.add(l.sum(), y.numpy().size) or metric.add(l*len(y), y.numpy().size)?
why we so care about size?
Why does metric[0] / metric[1] represent loss?
In my pics, the distance of the orange line and the blue line is so near.
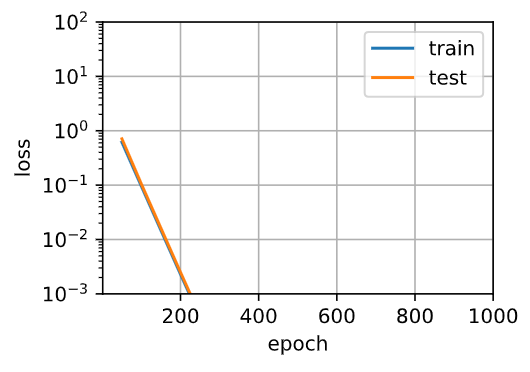
And overfitting that test loss increases did’t happen!
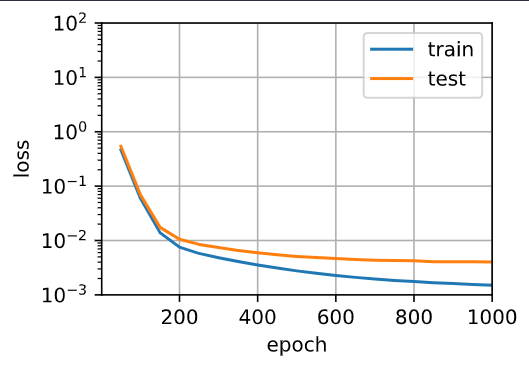
Why?
-
I don’t know what exactly means?
-
(1) By model complexity increasing, the training error will decrease. TODO:
(2) TODO:
(3)a function of the amount of data? what function you mean? -
I haven’t figure out the meaning of the question. ? The new polynomial features will multiply i!.
-
Just as same as the number of all points.
-
I can expect if I really understand the patterns of all data whether it is trained or not.
Hi @StevenJokes,
what Accumulator really do ?
It is an efficient way to “sum a list of numbers over time” for accumulated loss and accuracy calculation over all epochs.
Why does
metric[0] / metric[1]represent loss ?
So the first item means the total loss (over all the mini-batch and all the epochs), and if we divided by the total number of examples through all the epochs (one training example will be passed n times if epoch=n)
But, I am still curious about the necessity of float() and what args represents.
Why metric.add(l.sum(), y.numpy().size) or metric.add(l*len(y), y.numpy().size) ?
why we so care about size ? Does metric[1] represent epoch_num?
Sometime in the last minibatch, we don’t have the sample as the minibatch size. Hence, we may act differently based on our needs: we can
- drop the last “inadequate” minibatch
- fill the last minibatch with some extra samples at the beginning
- process this “inadquate” minibatch directly
Hence, to deal with the cases universally, we need to accumulate the sum and size at the same time.
The functions to your methods(  Am I right?):
Am I right?):
- Corresponding with the first method is DataLoader(Drop_Last = True)?
- How to fill?
- DataLoader(Drop_Last = False)
the necessity of float() in def add ,
self.data = [a+float(b) for a, b in zip(self.data, args)]?
Why metric.add(l.sum(), y.numpy().size) or metric.add(l*len(y), y.numpy().size) ?
x.nelement()in pytorch is like x.size in numpy.
https://pytorch.org/docs/master/generated/torch.nn.MSELoss.html
return vector(batch_size, ) .
Would you like to tell me the meanings of l.sum () or l*len(y) in more details?
Hi @StevenJokes,
You can choose last_batch in {‘keep’ , ‘discard’ , ‘rollover’} ) in DataLoader (https://beta.mxnet.io/api/gluon/_autogen/mxnet.gluon.data.DataLoader.html).
I’m learning pytorch.https://pytorch.org/docs/stable/data.html
Am I right?DataLoader(drop_last = False)
https://beta.mxnet.io/guide/getting-started/to-mxnet/pytorch.html is helpful!
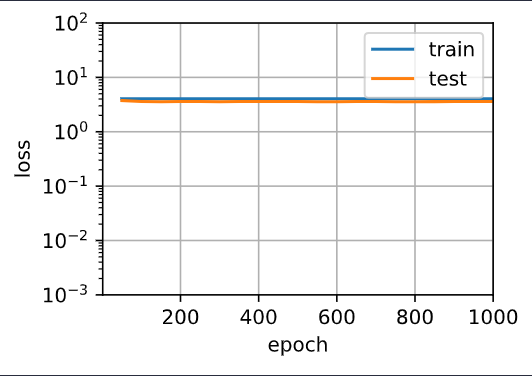
@goldpiggy I don’t understand how underfitting is happening when we limit our polynomial degree to 3. I understand that the labels that we generated were made using poynomial of degree 4 and we are trying to train the 3 degree polynomial to get labels that are close to those generated by 4 degree polynomial and hence our model will be inaccurate. But how does underfitting relate to this? What characteristic of underfitting is shown by this model?
@goldpiggy
Also, in section 4.4.4.4,
# Pick the first four dimensions, i.e., 1, x from the polynomial features
train(poly_features[:n_train, 0:3], poly_features[n_train:, 0:3],
labels[:n_train], labels[n_train:])
Since we are trying to fit a linear model to demonstrate underfitting as per the heading, shouldn’t we be picking the first two dimensions (not the first four dimensions as stated in the comment in the code) and choose train_features and test_features to be poly_features[ :n_train, 0:2] and poly_features[ n_train:, 0:2]?
small typo in the exercises:
- question:
“Concider” -> “Consider”
Great call! Feel free to fix it over a PR and be our contributor!  https://d2l.ai/chapter_appendix-tools-for-deep-learning/contributing.html
https://d2l.ai/chapter_appendix-tools-for-deep-learning/contributing.html
I can’t display the animation in VS Code. Anyone knows how to solve it?