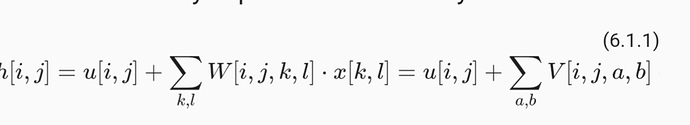http://d2l.ai/chapter_convolutional-neural-networks/why-conv.html
6.1.2 formulas make use of the u[i,j] term but there is no explanation of what is u.
Equation 6.1.1 is missing the x term that multiplies V.
6.1.6.2 When might it not make sense to allow for pigs to fly?
What does “when” mean?
6.1.1 formulas make use of the u[i,j] term but there is no explanation of what is u .
Wait for explanation.
6.1.2 formulas make use of the u[i,j] term but there is no explanation of what is u .
Hi @lregistros and @StevenJokes, u is the bias term here. Sorry for confusion, we will rewrite this section later.
Because these networks are invariant to the order of the features, we could get similar results regardless of whether we preserve an order corresponding to the spatial structure of the pixels or if we permute the columns of our design matrix before fitting the MLP’s parameters.
7. Convolutional Neural Networks — Dive into Deep Learning 1.0.3 documentation §1
This would require to permute the columns for all examples consistently or could we basically shuffle all examples in a different way for the same training run?
Couldn’t understand your meaning. Do you mean whether we keep order of examples or not?
If you ask this, the answer is not.
No, that wasn’t the question.
Hi @manuel-arno-korfmann, great question! We need to permute the columns for all examples consistently. Since features’ sequence is important for NN, once the weights are trained. Each feature should come from specific location. Even though for the feature themselves, their order is not important.
I can’t see why equation 6.1.1 where sum over (k,l) of [W]i,j,k,l [X]k,l is the same as sum over (a,b) of [W]i,j,a,b [X]i+a,j+b ?
I believe that the first part is clear about how “every” pixel of X is going to contribute to “every” pixel of H. Isn’t the second part limits the contribution of X to H on just “some part” of X based on the position of (i,j) which I believe what a convolution is?
I just don’t see why it’s mathematically correct?!
Hi @osamaGkhafagy, it is not too complicated, just replace the following in 6.1.1:
- set 𝑘=𝑖+𝑎, 𝑙=𝑗+𝑏;
- set [𝖵]𝑖,𝑗,𝑎,𝑏=[𝖶]𝑖,𝑗,𝑖+𝑎,𝑗+𝑏.
Well, then we will have to change the limit we sum over from (k,l) to (i+a, j+b)!
We now conceive of not only the inputs but also the hidden representations as possessing spatial structure.
So does this mean that each perceptron in our hidden layer is two-dimensional much like our input image?
Also, why does our weight matrix W have to be a 4th order tensor? If our input X is a two dimensional matrix and we are multiplying W with it, shouldn’t W be a two dimensional matrix as well?
Hi @Kushagra_Chaturvedy, great question! Here we assume we have (𝑘,𝑙) neurons, and each neuron has “i x j” weights. These weights can be in 1d or 2d dimension. If we reshape them to 2d, that will be the convolution kernel. Let me know if it makes sense to you!
Hi,
In equation 6.1.1, weight has been indexed with i, j, k, l and X has been indexed with just k and l. However, X is the input and based on which H[i][j] is produced, thus, shouldn’t the X be indexed with i and j. And, further computation is centered on ith and jth of X. Thus, I suppose the indexing of W and X should be other way around.
Thanks,
Jugal
What does it mean to have (k, l) neurons? and each neurons has “i*j” weight? and why setting k = i+a and l=j+b but we don’t change the limit of the sum? that is we should have W(i, j, i + a, j + b)*X(i + a, j + b), sum over k = i +a and l = j + b
Hi @goldpiggy, can you please clarify your comment? What does it mean to have (k,l) neurons? And it seems to me that what @jugalraj is asking also makes sense. Could please take another look at 6.1.1? There is either a typo there or probably the explanation should be a bit more detailed. Thanks!