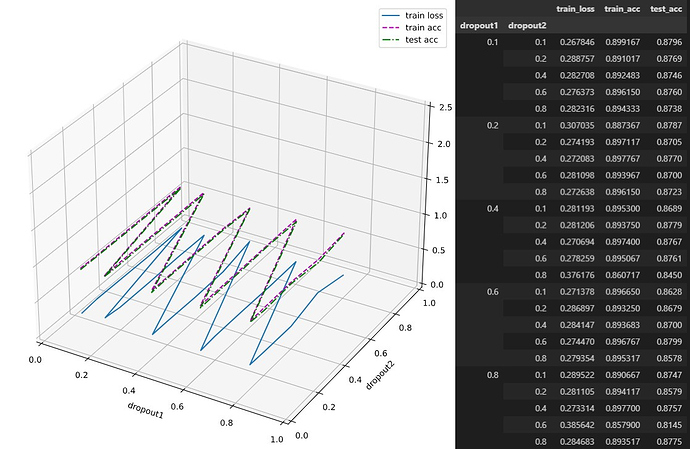
In exercise 2 of 4.6.7, I increase the epochs to 100 with dropout1 and dropout2 (0.2/0.5), run several times. In each time, always got a result with train/test acc having a dropping part during training. In my knowledge, if increasing the epochs with other appropriate parameters, the result should be better, but not worse. See the below results:
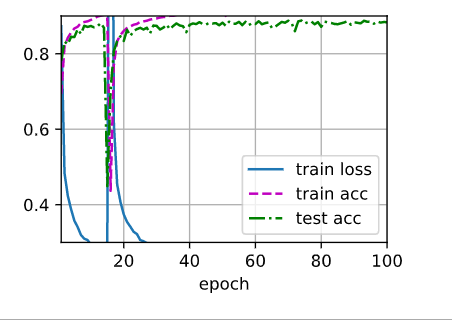
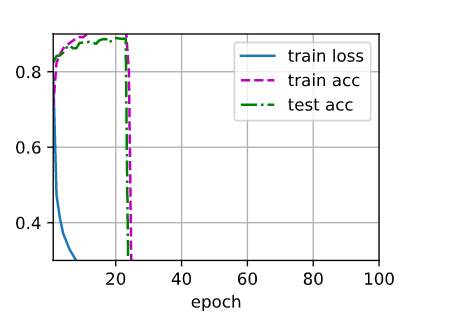
Is there any theory to explain the result? ( I saw there was a student having the same problem using pytorch)
- What happens if you change the dropout probabilities for the first and second layers? In particular, what happens if you switch the ones for both layers? Design an experiment to answer these questions, describe your results quantitatively, and summarize the qualitative takeaways.
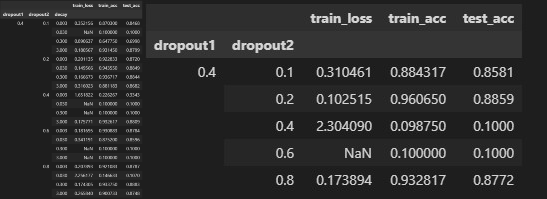
Below are the results when dropout rates are switched(tabular format for more clarity)
- Using the model in this section as an example, compare the effects of using dropout and weight decay. What happens when dropout and weight decay are used at the same time? Are the results additive? Are there diminished returns (or worse)? Do they cancel each other out?
The weight decay, when used along with dropout, is at times additive and diminishing as seen from the table below.
Hello, this is my first question.
I’m just wondering that the dropout procedure is not conducted in Section ‘4.6.4.3’.
As we can see from the user-defined funtion ‘Net()’ in Section ‘4.6.4.2’, the default value of the option ‘training’ is given as ‘none’.
Can anyone tell me whether I am on the right track?
Thank you.
So, the alternative codes that I’ve considered are the slight modifications of the ‘train_epoch_ch3()’ funtion and ‘train_ch3()’ function in d2l module into ‘train_epoch_dropout()’ and ‘train_dropout()’, which are defined as follows:
def train_epoch_dropout(net, train_iter, loss, updater):
"""The training loop defined in Chapter 3."""
# Sum of training loss, sum of training accuracy, no. of examples
metric = d2l.Accumulator(3)
for X, y in train_iter:
# Compute gradients and update parameters
with tf.GradientTape() as tape:
y_hat = net(X, training=1)
# Keras implementation for loss takes (labels, predictions)
# instead of (predictions, labels) that users might implement
# in this book , e.g. 'cross_entropy()' that we implemented above.
if isinstance(loss, tf.keras.losses.Loss):
l = loss(y, y_hat)
else:
l = loss(y_hat, y)
if isinstance(updater, tf.keras.optimizers.Optimizer):
params = net.trainable_variables
grads = tape.gradient(l, params)
updater.apply_gradients(zip(grads, params))
else:
updater(X.shape[0], tape.gradient(l, updater.params))
# Keras loss by default returns the average loss in a batch
l_sum = l * float(tf.size(y)) if isinstance(
loss, tf.keras.losses.Loss) else tf.reduce_sum(l)
metric.add(l_sum, d2l.accuracy(y_hat, y), tf.size(y))
# Return training loss and training accuracy (sample mean version)
return metric[0] / metric[2], metric[1] / metric[2]
def train_dropout(net, train_iter, test_iter, loss, num_epochs, updater):
"""Train a model (defined in Chapter 3)."""
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
train_metrics = train_epoch_dropout(net, train_iter, loss, updater)
test_acc = d2l.evaluate_accuracy(net, test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc