Dropout

English Version pytorch
11

I noticed there isn’t test loss. Why?
I have read as following.


https://kharshit.github.io/blog/2018/12/07/loss-vs-accuracy
12

I noticed that nn.Flatten() haven’t mentioned.
https://pytorch.org/docs/master/generated/torch.nn.Flatten.html
Why do we need to nn.Flatten() first?

13

Two pics in 4.6.4.3. Training and Testing and 4.6.5. Concise Implementation are so different?

4.6.7. Exercises

  1. I have tried to switch the dropout probabilities for layers 1 and 2 by switching dropout1 and dropout2.
    Sequential(
    (0): Flatten()
    (1): Linear(in_features=784, out_features=256, bias=True)
    (2): ReLU()
    (3): Dropout(p=0.5, inplace=False)
    (4): Linear(in_features=256, out_features=256, bias=True)
    (5): ReLU()
    (6): Dropout(p=0.2, inplace=False)
    (7): Linear(in_features=256, out_features=10, bias=True)
    )
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

4-6e-1
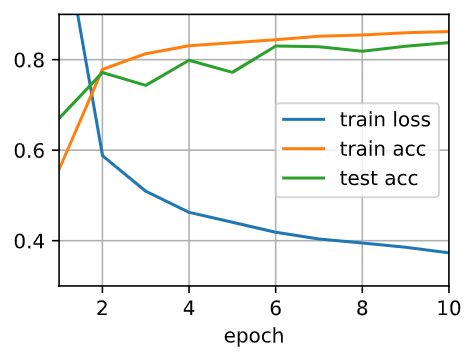
But how can I confirm that the change’s cause is my action of switching the dropout probabilities other than random init?

num_epochs = 20
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

4-6e-2
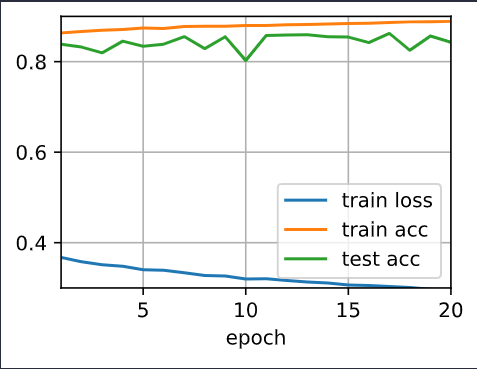
d2l.train_ch3? Does it train continously? I guess so.

14

You need to reset params before you start training again.
Otherwise you are just updating already trained params.

Also nn.Flatten() is needed to flatten the image into a single vector (28*28=784) for the input of the linear layer.

Cam you check again 4.6.5 and 4.6.4.3 look similar here.

15

we use .reset_parameters()?

And I found that searching in pytorch docs is so slow. Do you have some good advices?

How similar can we say that these pics are similar?
We can’t expect exactly the same outputs when we have the same inputs?

16

Hi @StevenJokes, for your question:

I noticed there isn’t test loss. Why?

For any ML problem, we ultimately care about the model performance through evaluation metrics (such as accuracy). However, lots of metrics are not differentiable, hence we use the loss functions to approximate them.

17

We use loss function just for training’s Backpropagation, and we don’t need to train anymore when we are in test. Similiarly, we just care the final scores of exam instead of the concrete answers.
Do I understand it rightly?

18

@goldpiggy In this discussion thread, you refer to “model capacity”. What exactly does it mean?

19

I tried swapping the dropout probabilities for Layers 1 and 2, and did not notice much of a change:

image
image1066×1628 163 KB

Is there an error in my implementation? Or is this because of the simple nature of the dataset (eg I note that dropout doesn’t help too much over the standard implementation in the first place) and would I normally notice some difference? Thanks!

20

Hi @Nish, great question! It may be hard to observe a huge loss/acc difference if the network is shallow and can converge quickly. As you can find in the original dropout paper (http://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf) as well, the improvement with dropout on MNIST is less than 1%.

2 Likes
21

Hi, I’ve noticed that we enable Dropout while training, and we may disable it while doing inference. But whether we enable or disable Dropout while testing? If I am not mistaken, in our implementation, we have allowed Dropout in the test. Is that right?

Also, I have another question. We implement Dropout just by zeroing some elements in the forward stage, but whether the weights corresponding to those zeros update in the backward stage?

22
  1. We don’t allow Dropout in the test.
    The first answer in
    How does dropout work during testing in neural network? can explain well.

However, there are two main reasons you should not use dropout to test data:

  • Dropout makes neurons output ‘wrong’ values on purpose
  • Because you disable neurons randomly , your network will have different outputs every (sequences of) activation. This undermines consistency.
  1. the weights corresponding to those zeros will still update, because the weight not only corresponds to those zeros, but also other not zeros in the same hidden layer.
1 Like
23

Thanks for your answer. But I’m still wondering for something:

  1. How we disable Dropout in testing in the implementation of this book, either from scratch or using high-level API? I’ve found in the implementation from scratch that during training and testing we use the same net, whose attibute is_training is to True. Also, in the implementation using high-level API, I didn’t find the difference of Dropout layer while training and testing.
    So could you please tell me where in the code did we disable Dropout while testing?

  2. because the weight not only corresponds to those zeros, but also other not zeros in the same hidden layer.

    Is this means each weight corresponds to multiple hidden units? I’m not sure about this, but I think each weight corresponds to a unique input (hidden units) and a unique output in MLP.

24
  1. After we dropouted, the corresponding hidden layers have already changed. Enable/Disable is confusing.
    Test is just a process of calculating a prediction by weights after bp. We don’t need to disable Dropout!
  2. Yes, matrix multiplication is the reason of corresponding to multiple hidden units.
25

More intuitively, we might argue that we encouraged the model to spread out its weights among many features rather than depending too much on a small number of potentially spurious associations.

In the interactive example from google’s crash course I’m seeing roughly the same amount of features being used when comparing training the model with and without L2 regularization/weight decay:

This means I couldn’t verify the claim or intuition that weight decay spreads out it’s weight among many features.

26

What is the variance of the activations in each hidden layer when dropout is and is not applied? Draw a plot to show how this quantity evolves over time for both models.

Is the number of hidden units that are activated the subject of the question or the numerical outputs of the hidden units?

27

Hi,
I’m a bit confused between Dropout and Regularization. Should we use them both to train a neural network or one method is enought.

I tried using L2 regularizaion with Drop out in the exmaple in the book but I got an error

let’s leverage the efficient built-in PyTorch weight decay capability

def train_concise(wd):
#net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
# Add a dropout layer after the first fully connected layer
nn.Dropout(dropout1),
nn.Linear(256, 256),
nn.ReLU(),
# Add a dropout layer after the second fully connected layer
nn.Dropout(dropout2),
nn.Linear(256, 10))

net.apply(init_weights)
for param in net.parameters():
    param.data.normal_()
loss = nn.MSELoss()
num_epochs, lr = 100, 0.003
# The bias parameter has not decayed
trainer = torch.optim.SGD([
    {"params":net[0].weight,'weight_decay': wd},
    {"params":net[0].bias}], lr=lr)
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                        xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
    for X, y in train_iter:
        with torch.enable_grad():
            trainer.zero_grad()
            l = loss(net(X), y)
        l.backward()
        trainer.step()
    if (epoch + 1) % 5 == 0:
        animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                 d2l.evaluate_loss(net, test_iter, loss)))
print('L2 norm of w:', net[0].weight.norm().item())

The error says “‘Flatten’ object has no attribute ‘weight’”. Can someone explain this to me???

28

Do different neurons get dropped out during different training epochs? For example, if the first and last neurons of a layer are dropped out in the first forward pass, a gradient is eventually calculated at the output and then backpropagated. When the second forward pass starts, do the same neurons that were dropped out during the first forward pass get dropped out? Or a different set of neurons drop out?

Thanks!

29

Hi @tinkuge, great question. A different set of neurons will be dropped out (or turned off), i.e., we don’t include them in calculation but temporarily froze their weights.

2 Likes
30

image
image1630×810 82 KB

By plot the train loss and accuracy where drop_out1 from 0 to 1, I find that the train loss is relatively low, train acc and test acc is relatively high when drop_out1=0.2. Similarly, the overall training results is best when drop_out2=0.5. Is it right? @goldpiggy