Dropout

[mli]

http://d2l.ai/chapter_multilayer-perceptrons/dropout.html

[VolodymyrGavrysh]

1. What happens if you change the dropout probabilities for the first and second layers? In
   particular, what happens if you switch the ones for both layers? Design an experiment to
   answer these questions, describe your results quantitatively, and summarize the qualitative
   takeaways.

Answer
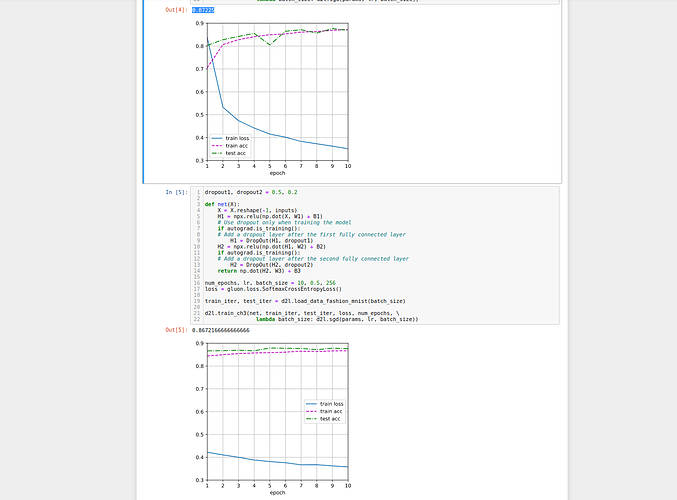
1.1 Here is the result if we switch Dropout coeff.

So, we have a bit drop in accuracy

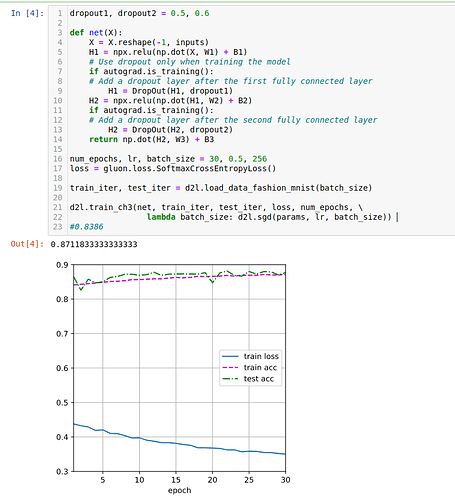
2.2 After iterate over, a pair of dropout coeff. I have next result:

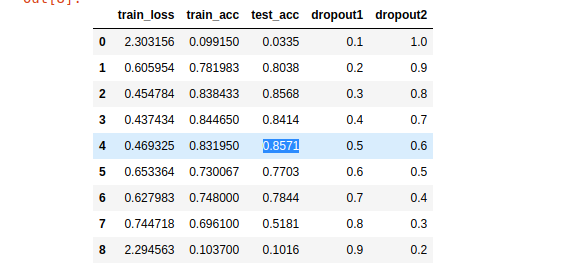
As you may see, the best test accuracy we have with next combination of drop out - (0.5, 0.6)

Here is the result in graph with that dropout coeff.

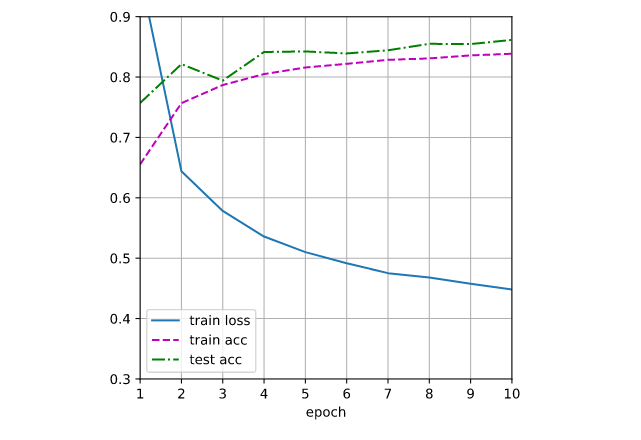
General rule that can be learned from -> we can find the best dropout coeff. via grid search as we usually for hyperparameters.

[VolodymyrGavrysh]

2. Increase the number of epochs and compare the results obtained when using dropout with
   those when not using it.

Asnwer -> More epochs helps to improve test metric. In my case it was +3%

[VolodymyrGavrysh]

4. Why is dropout not typically used at test time?

Answer
Perhaps using dropout to test the accuracy of the model on a test sample will distort the result because

• 1. We set probabilities without reference to the model, making our own assumptions.
• 2. The way we apply dropout to the weights (w) of the model is also random (in the example, uniform distribution is selected)

---

5. Using the model in this section as an example, compare the effects of using dropout and
   weight decay. What happens when dropout and weight decay are used at the same time?
   Are the results additive? Are there diminished returns (or worse)? Do they cancel each other
   out?

Answer

5.1 Here is log of experiments (fashion_mnist data with fixed lr=0.1, batch size=256 and 10 epoch)

test acc 0.7335 -> l2_coeff = 0.50 -> dropout1, dropout2 = 0, 0
test acc 0.7904 -> l2_coeff = 0.10 -> dropout1, dropout2 = 0, 0
test acc 0.8298 -> l2_coeff = 0.01 -> dropout1, dropout2 = 0, 0
test acc 0.8162 -> l2_coeff = 0.01 -> dropout1, dropout2 = 0.4, 0.5
test acc 0.8145 -> l2_coeff = 0.00 -> dropout1, dropout2 = 0.4, 0.5
test acc 0.8487 -> l2_coeff = 0.00 -> dropout1, dropout2 = 0.4, 0.6
test acc 0.8602 -> l2_coeff = 0.00 -> dropout1, dropout2 = 0.5, 0.6
test acc 0.8057 -> l2_coeff = 0.10 -> dropout1, dropout2 = 0.5, 0.6
test acc 0.8374 -> l2_coeff = 0.01 -> dropout1, dropout2 = 0.5, 0.6
test acc 0.8598 -> l2_coeff = 0.001 -> dropout1, dropout2 = 0.5, 0.6
test acc 0.8570 -> l2_coeff = 0.0001 -> dropout1, dropout2 = 0.5, 0.6

If we use dropout and WB together we have almost the same results as using only dropout. That result could depend on the data itself and other parameters (like initial weights, lr, batch size)

But generally for noisy data dropout + wb could help to increase metric. After certain level the growth of those both hyperparameters would worsen the results, so we could find the best combination via grid search