“the denominator is contained in the interval [1, q]”
How is the interval [1, q] calculated?
Here are my opinions for the exercises:
ex1:
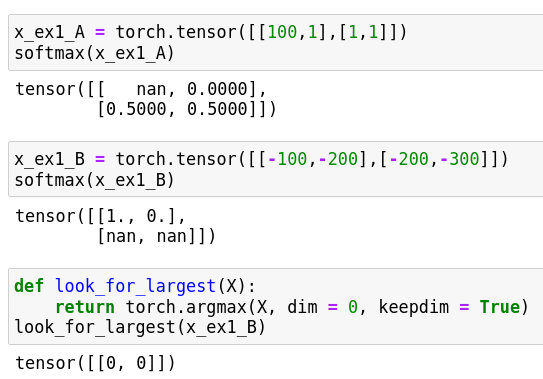
ex2
The true cross-entropy function that compute each -log(y_hat) * y, that is good for some other condition, but waste more time cause I only need to compute the not zero y in one-hot programming.
ex3:
I may set a threshhold like 10%, if I get more than one label that has a possibility of more than 10%, then I will assume the patient has all these kind of disease.
ex4
If I still consist to use one-hot programming, I will face the fact that my label vector is very long and has many zero for each example.
I want to share some insights, that boggled my mind for quite some time.
I always understand how the log-sum-exp trick avoids positive overflows on large positive exponents (Answer: by taking out the max element)
I found it tricky to see how the trick avoids negative overflows when there are on very negative exponents ex: o_j = -5000 — especially, then the largest exponent is positive, such as bar{o}=+5000 )**
In this case o_i -bar{o} is something very negative (like -10000), and YOU WOULD THINK that if all terms in the sum are like that, their exp(oi-bar{o}) is near zero, and after summation you may end up taking a log of essentially zero then in the extreme case you get log(0)=negative infinity.
NO NEED TO WORRY: You are saved by the fact that at least one term (the one where o_i=\bar{o}) will have an exponent of 0, leading to exp(0)=1. And log(1 + near zeros) > 0
** Note: There is a lot of misleading information on the internet claiming that \bar{o} is always negative, which is true for log probabilities, but not true for logistic regression where the softmax is applied to a linear model with unconstrained weights.
Y_hat = Y_hat.reshape((-1, Y_hat.shape[-1]))
Y = Y.reshape((-1,))
what is the point of these lines. seems to work the same without it
Y_hat = Y_hat.reshape((-1, Y_hat.shape[-1]))
This is to keep the last dimension of Y_hat unchanged while collapsing other dimension into a single one
Y = Y.reshape((-1,))
This flattens Y into an array.
Such shapes are required for cross_entropy function (see Shape section in the doc)
If it seems to work the same even without those reshape, it’s probably because the shape is already good before reshape