Great question @Philip_C! Since we are optimizing 𝑦̂ to a range of [0,1], we didn’t expect “exp()” to be a super large number. This LogSumExp trick is to deal the overflowed numerator and denominator.
Thank you for your reply!
But I still have questions here. ∑𝑘exp(𝑜𝑘) is still calculating the exp() of the logit O, which can still be a large number, thus having the same overflow issue, right?
I want to give a more specific example about why I still don’t understand this trick. For example, let’s assume that we have a logit outcome coming from the model as O = tensor([[-2180.4433, -1915.5579, 1683.3814, 633.9164, -1174.9501, -1144.8761, -1146.4674, -1423.6013, 606.3528, 1519.6882]]), which will become the input of our new LogSumExp Trick loss function.
Now, in our loss function in the tutorial, we have the first part Oj, which do not require exp() calculation. Good. However, we still have the part exp(Ok) in the second part of the new loss function and this part still requires the exp() calculation of every element of the logit outcome O. Then we will still have the overflow issue, e.g. for the last element of O, we will have an overflow error for exp(1519.6882).
This is the part I am still confused. Thank you!
Hi @Philip_C, great question! Logsumexp is a trick for overflow. We usually pick the largest number in the tensor as o_j. i.e., we choose ![]() in
in 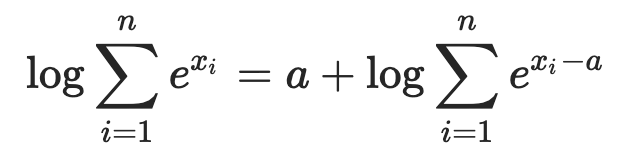 . Please see more details here.
. Please see more details here.
Thank you! I got it now. I have to subtract the largest value a from it. I misunderstood it as I thought you don’t have to do that and it was another failed solution.
Hi there,
I have copied the code precisely for both this tutorial and the previous one into an IDE (VS Code), and though it runs without errors, it does not produce any visualisations as depicted. It simply completes running silently. Are the graphs only available in a jupyter-like notebook environment?
Exercises
- Try adjusting the hyperparameters, such as the batch size, number of epochs, and learning
rate, to see what the results are.
- changing batch_Size increases time, more epochs trainingaccuracy is more or less constant, learning rate we have to try, changing to 1 loss increases, 0.01 converges slowly.
- Increase the number of epochs for training. Why might the test accuracy decrease after a
while? How could we fix this?
- maybe overfitting
They are not available only in jupyter notebooks, however jupyter does have a special way of displaying plots that makes things much easier.
When I use the PyCharm IDE I have to use either scientific mode, save the plots to a file (ie png), or debug the line of code containing “fig.show()” to view my plots. These are the only solutions I have found so far in PyCharm. Hope that helps!
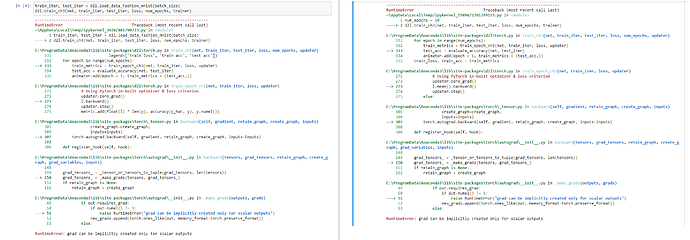
Could you please help me with the following issue: when trying to run d2l.train_ch3 in this notebook, I get the error as in the left side of the attached picture. I realized that the package d2l does not contain the correct train_epoch_ch3 function, so I copied the correct one (from the 3.6 jupyter notebook) into the d2l package file. However, the error persists, as shown in the right side of the picture. Can you please offer some assistance?
when i saw this error i saw that in the pytorch discusion they indicated that this is most probably due to the loss being a multidementional tensor and that the solution is to “perform some reduction or pass a gradient with the same shape as loss.”
I then just changed the code in the CrossEntrypyLoss function to remove the reduction = ‘none’. The code then ran fine after that and i saw similar results in training to Softmax regression from scratch.
loss = nn.CrossEntropyLoss()
When running in an IDE or from the command line you can display the matplotlib plots by adding “import matplotlib.pyplot as plt” to the imports and then “plt.show()” at the end. This is enough to get the plots displayed when plt.show() is reached (e.g. at the end)
If you want the plots updated after each epoch, then add plt.ion() to put matplotlib into interactive mode, and then plt.pause(0.02) whenever you want the plot updated (for example at the end of each epoch). This allows matplotlib’s GUI loop to run for long enough (0.02s for example) to redraw the plot. At the end, you can say plt.show(block=True) to keep the plot visible if that’s what you want.
“the denominator is contained in the interval [1, q]”
How is the interval [1, q] calculated?
Here are my opinions for the exercises:
ex1:
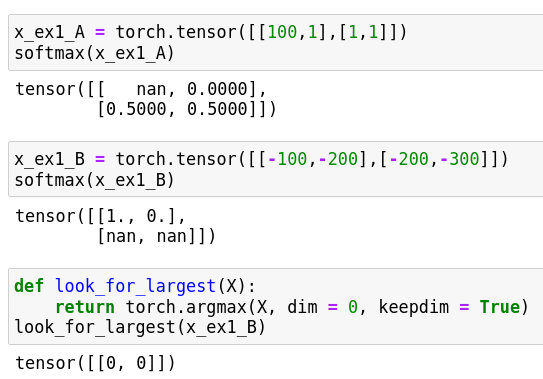
ex2
The true cross-entropy function that compute each -log(y_hat) * y, that is good for some other condition, but waste more time cause I only need to compute the not zero y in one-hot programming.
ex3:
I may set a threshhold like 10%, if I get more than one label that has a possibility of more than 10%, then I will assume the patient has all these kind of disease.
ex4
If I still consist to use one-hot programming, I will face the fact that my label vector is very long and has many zero for each example.
I want to share some insights, that boggled my mind for quite some time.
I always understand how the log-sum-exp trick avoids positive overflows on large positive exponents (Answer: by taking out the max element)
I found it tricky to see how the trick avoids negative overflows when there are on very negative exponents ex: o_j = -5000 — especially, then the largest exponent is positive, such as bar{o}=+5000 )**
In this case o_i -bar{o} is something very negative (like -10000), and YOU WOULD THINK that if all terms in the sum are like that, their exp(oi-bar{o}) is near zero, and after summation you may end up taking a log of essentially zero then in the extreme case you get log(0)=negative infinity.
NO NEED TO WORRY: You are saved by the fact that at least one term (the one where o_i=\bar{o}) will have an exponent of 0, leading to exp(0)=1. And log(1 + near zeros) > 0
** Note: There is a lot of misleading information on the internet claiming that \bar{o} is always negative, which is true for log probabilities, but not true for logistic regression where the softmax is applied to a linear model with unconstrained weights.
Y_hat = Y_hat.reshape((-1, Y_hat.shape[-1]))
Y = Y.reshape((-1,))
what is the point of these lines. seems to work the same without it
Y_hat = Y_hat.reshape((-1, Y_hat.shape[-1]))
This is to keep the last dimension of Y_hat unchanged while collapsing other dimension into a single one
Y = Y.reshape((-1,))
This flattens Y into an array.
Such shapes are required for cross_entropy function (see Shape section in the doc)
If it seems to work the same even without those reshape, it’s probably because the shape is already good before reshape
I have a question that should be pretty simple…
Where are the graph plottted? I searched thed2l train class without success.
Thanks
OK, I solved my problem…
To get the figure to update, I added these two lines:
d2l.plt.draw()
d2l.plt.pause(0.01)
at the line 211 of torch.py of d2l.
This is at the end of the Module.plot function.
OK, I solved this problem…
To get the figure to update, I added these two lines:
d2l.plt.draw()
d2l.plt.pause(0.01)
at the line 211 of torch.py of d2l.
This is at the end of the Module.plot function.