Calculus

English Version tensorflow
1

http://d2l.ai/chapter_preliminaries/calculus.html

2

Exercise 1

The derivative of:

\ x^3-\frac{1}{x}
is:

\ 3x^2-(-\frac{1}{x^2}

At x = 1 we get y = 0 and a slope for the tangent of 4
The tangent will have an intercept of -4 and an equation of 4x-4

To plot:

def f(x):
    return(x**3-1/x)

#div by 0 error at x=0, so we use x=0.1 
x = np.arange(0.1, 3, 0.1)
fig = plot(x, [f(x), 4 * x-4], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

The image will be:
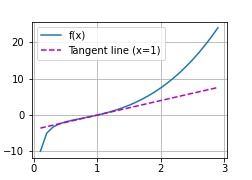
2_Prelim 4_Calc 1_Ex

To save this image add this line to the beginning of the plot function:

    fig = d2l.plt.figure()

and a return to the end:

    return fig

and this after making the plot:

fig.savefig("2_Prelim 4_Calc 1_Ex.jpg")
1 Like
3

Exercise 2

1 Like
4

I appreciate any corrections!

Exercise 3

Explaination:

use the chain rule:

Exercise 4

1 Like
5

Your solution is so brief and correct. Thank you :slight_smile:

6

I think part (2.4.8) needs clarification.
The first bullet point states that for any matrix “A” in R(m x n) and vector “x” in Rn, the gradient of (Ax) is A^T.
What does that mean? Do we treat A as a linear transformation function from Rn to Rm? How do you take the gradient of that? Why does it equal to A_T (Rn x m vector)? I missed the generalization from how the gradient was defined (vector of partial derivatives of a function whose domain is Rn and range is R).
Moving on, I didnt understand how can x_T be multiplied by A ? x_T is of (1 x n) shape and A is (m x n), the dimensions don’t match.
The second bullet point mentions the gradient of the square of the norm of x. I understand this is equivalent to x_T * Identity (nxn) * x, but again I seem to not understand the notation here, it seems like we are taking the gradient of a scalar (||x||^2 is a scalar how can we take the gradient of that)?

1 Like