Why do we need moving average (the average of average for every mini batch) for prediction mode? Instead we can do, once we finished training the model, we calculate the whole dataset average and use it for batch normalization in prediction mode. And the momentum part in the moving average formula, is it smoothed moving average formula? Also you should write epsilon rather than eps in code just in case to make it more concise. Thank you.
Hey @rezahabibi96, great question! Your question is fundamentally asking the
choice of batchsize (since for the “mini-batch”, it uses the mini batch size to normalize each sample; while for the “whole dataset” batch, it uses the whole training sample size to normalize each sample.) As we mentioned in this section: “One takeaway here is that when applying batch normalization, the choice of batch size may be even more significant than without batch normalization”. If we use the mini batchsize, then the variance decreases and the benefit of the noise-injection drops. Check more details on http://d2l.ai/chapter_optimization/minibatch-sgd.html#minibatches. Let me know if it helps?!
What exactly are you asking for in exercise 2?
“Compare the learning rates for LeNet with and without batch normalization.”
Is it an experiment which a high and low learning rate with and with out batch normalization? Or is it just 1.) the given learning rate, with and without batch norm and 2.) how large can you make the learning rate with batch normalization?
Hi @smizerex, great question. Sorry for a bit confusion. Would it be more clear if we state it this way:
Cool, thank you  !
!
What defines a “maximum learning rate”? for both models i was able to put in learning rates much larger than 1000 and the models not blow up. Once iI got to learning rates that generated training and test accuracy around .1, accuracies were varying from .1-.2 which I wasnt sure if that was just from the resolution dilution from having error and accuracy on the same graph.
There seems to be a discrepancy regarding the LeNet specified here vs the one specified in 6.6 –
the LeNet here uses MaxPooling, while the original uses AvgPooling.
You want to control for pooling while considering Batch Normalization’s effect.
Furthermore simply changing the original LeNet from Avg -> Max Pooling yields an accuracy increase from:
(Avg) loss 0.467, train acc 0.824, test acc 0.797
->
(Max) loss 0.411, train acc 0.849, test acc 0.841
Versus the BatchNormalization scores reported in this chapter hovering around:
loss 0.250, train acc 0.909, test acc 0.849
It would seem most of the effect is explained by the choice of Pooling rather than the application of Batch Normalization.
but even I remove all pools and the 120 layer, the result is much more accurate.
when i run neural networks on my GPU( NIVIDIA RTX), the model can’t learn. let me show some instances: the result from applying batch normalization in LeNet as shown below
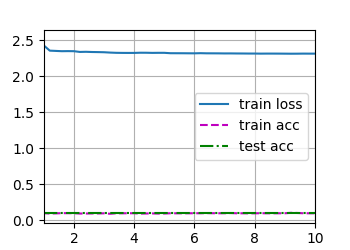
is there anyone who can help me to figure out ? thank you
@goldpiggy The first convolution layer in this section is different then in 6.6: it’s missing padding=2. Is this on purpose?
http://d2l.ai/chapter_convolutional-neural-networks/lenet.html#lenet