It’s a typo. Thanks for fixing it!
can u explain the difference btw formula 8.7.4 and 8.7.16 . why in 8.7.16 we dont need to compute
∂ht/∂Whx like what u did in 8.7.4 recurrently ?
I think you misunderstood that. It is noted that:
So, the Derivative is related to the w_h and h_{t-1}
I had a question on Truncating Time Steps
Alternatively, we can truncate the sum in [(8.7.7)](http://d2l.ai/chapter_recurrent-neural-networks/bptt.html#equation-eq-bptt-partial-ht-wh-gen) after 𝜏 steps. This is what we have been discussing so far, such as when we detached the gradients in [Section 8.5](http://d2l.ai/chapter_recurrent-neural-networks/rnn-scratch.html#sec-rnn-scratch). This leads to an *approximation* of the true gradient,
So if I analyze the code in 8.5 are we detaching it at each time step?
#@save
def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):
"""Train a net within one epoch (defined in Chapter 8)."""
state, timer = None, d2l.Timer()
metric = d2l.Accumulator(2) # Sum of training loss, no. of tokens
for X, Y in train_iter:
if state is None or use_random_iter:
# Initialize `state` when either it is the first iteration or
# using random sampling
state = net.begin_state(batch_size=X.shape[0], device=device)
else:
if isinstance(net, nn.Module) and not isinstance(state, tuple):
# `state` is a tensor for `nn.GRU`
state.detach_()
else:
# `state` is a tuple of tensors for `nn.LSTM` and
# for our custom scratch implementation
for s in state:
s.detach_()
y = Y.T.reshape(-1)
X, y = X.to(device), y.to(device)
y_hat, state = net(X, state)
l = loss(y_hat, y.long()).mean()
if isinstance(updater, torch.optim.Optimizer):
updater.zero_grad()
l.backward()
grad_clipping(net, 1)
updater.step()
else:
l.backward()
grad_clipping(net, 1)
# Since the `mean` function has been invoked
updater(batch_size=1)
metric.add(l * y.numel(), y.numel())
return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()equation 8.7.16 seems to be wrong. dh(t)/dWhh != h(t-1), but equal to what’s expressed in equation 8.7.7. same for dh(t)/dWhx.
please correct me if there is some hidden assumption, thanks.
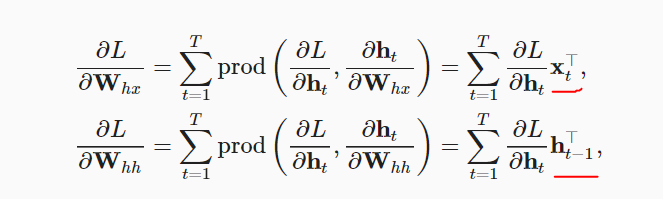
I think it should be an “=” too.
So do I. The first term is same as the second term.
perhaps he is referrind to dL/dw and not partial L / partial w
I think there should be a 1/2 term for both parts of the sum. That 1/2 term goes away when you keep going to the recurrence in 8.7.7.
Hi,
The “+” sign is correct after applying the chain rule for one independent variable.
Suppose that
- x = g(t) is differentiable function of t
- z = f(x, t) is differentiable function of x and t
Then, z = f( g(t),t ) is differentiable function of t and its derivative is:
- d(z)/d(t) = partial(z) / partial(x) . d(x)/d(t) + partial(z) / partial(y)
Back to the recurrent computation, as stating in the text that h_t depends on h_{t-1} and w_h while h_{t-1} also depends on w_h. Thus, if we see:
- h_t as z
- h_{t-1} as x
- w_h as t
we will have the formula 8.7.4.
I am also confused about this. Didn’t the first section discuss how dh_t / dW_hx needed to take into account the use of W_hx in the hidden states leading up to h_t?
Hi I think BPTT from 9.7.14 - 9.7.15 is wrong
I don’t know why the notation choice of this section is so bad.
Since h_t = f(x_t, h_(t-1), w_h), we can cancel the left term of Equation 8.7.4 with the first term of the right terms, making the last term of the right terms equal to zero.
All these nonsenses comes from the failed notation.
Although the authors state that the mathematical notation here does not explicitly distinguish between scalars, vectors, and matrices, this rather makes it hard to understand.
The author mis-used the total derivative with the partial derivative. The LHS of the equation should use total derivative symbol.
For chain rule with multi-variable functions, check (14.5.1) in the following link: 14.5: The Chain Rule for Multivariable Functions - Mathematics LibreTexts.
Great question . I found this issue too.
I think the first derivatives in section 8.7.1 is redundant to 8.7.2, and both are not consistent . so I mainly focus the latter
although it’s apparently wrong, I don’t think it can be fixed by simply replacing ‘+’ by ‘=’ . since Wh acts on both Xt and H[t-1] , that means this formula will loss one partial derivative w.r.t Xt. instead , I like the derivatives in section 8.7.2 .
this formular is correct wh has dependency on xt, because we concat wt with ht-1, so this part try to calculate derivative base on current xt.
remember, this is just a intuition as suggested in the beginning of this chapter
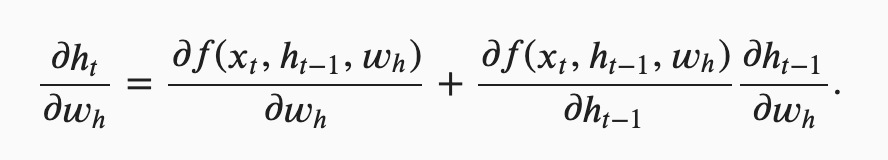
 here?while I think it’s = here.
here?while I think it’s = here.
