Correct me if i’m wrong, in (8.7.11), looks like the tanh activation was omitted, shouldn’t it be like below?
- z[t] = W_hh . h[t-1] + W_hx . x[t] + b
- h[t] = tanh(z[t])
Thus in (8.7.16), there is also a missing component of tanh derivative for each term in the sum which is product of (1 - tanh^2(z[i])) for i from t - j + 1 to t, i.e.
- (1 - h[t]^2)(1 - h[t - 1]^2)(1 - h[t - 2]^2) … (1 - h[t - j + 1]^2)
For reference, in Deepmind x UCL lecture on RNN, there is a similar formula with tanh component.
Hi @witx, great catch on the tanh function. We will fix it!
As for the missing bias term, we omit it for the sake of simplicity (similarly to https://d2l.ai/chapter_multilayer-perceptrons/backprop.html). You can think W = [b, w1,w2,…], and X = [1, x1, x2, …].
Hello,
Please correct me if I am wrong: in (8.7.16) if j runs from 1 to (t-1), shouldn’t the index be h_(j-1) instead of h_j from the previous equations (8.7.11). Would really appreciate the help!
Hi @Sharmi_Banerjee, great catch! Would you like to be a contributor and post a PR for this at github?
Sure I would love to. Submitted a PR. Thank you!
We just heavily revised this section:
Specifically, to keep things simple we assume the activation function in the hidden layer uses the identity mapping.
Can I ask why 8.7.2 need to do 1/t?
is that because of average the gradient between timestamp or have other purposes?
Yes, just average the gradient so the scale of loss won’t be sensitive to the length of sequences
Correct me if I am wrong, but I think I found a minor mistake in the last term of equation 8.7.3.
In particular, I believe that the top equation should be replaced with the bottom one in this screenshot of mine:
It’s a typo. Thanks for fixing it!
can u explain the difference btw formula 8.7.4 and 8.7.16 . why in 8.7.16 we dont need to compute
∂ht/∂Whx like what u did in 8.7.4 recurrently ?
I think you misunderstood that. It is noted that:
So, the Derivative is related to the w_h and h_{t-1}
I had a question on Truncating Time Steps
Alternatively, we can truncate the sum in [(8.7.7)](http://d2l.ai/chapter_recurrent-neural-networks/bptt.html#equation-eq-bptt-partial-ht-wh-gen) after 𝜏 steps. This is what we have been discussing so far, such as when we detached the gradients in [Section 8.5](http://d2l.ai/chapter_recurrent-neural-networks/rnn-scratch.html#sec-rnn-scratch). This leads to an *approximation* of the true gradient,
So if I analyze the code in 8.5 are we detaching it at each time step?
#@save
def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):
"""Train a net within one epoch (defined in Chapter 8)."""
state, timer = None, d2l.Timer()
metric = d2l.Accumulator(2) # Sum of training loss, no. of tokens
for X, Y in train_iter:
if state is None or use_random_iter:
# Initialize `state` when either it is the first iteration or
# using random sampling
state = net.begin_state(batch_size=X.shape[0], device=device)
else:
if isinstance(net, nn.Module) and not isinstance(state, tuple):
# `state` is a tensor for `nn.GRU`
state.detach_()
else:
# `state` is a tuple of tensors for `nn.LSTM` and
# for our custom scratch implementation
for s in state:
s.detach_()
y = Y.T.reshape(-1)
X, y = X.to(device), y.to(device)
y_hat, state = net(X, state)
l = loss(y_hat, y.long()).mean()
if isinstance(updater, torch.optim.Optimizer):
updater.zero_grad()
l.backward()
grad_clipping(net, 1)
updater.step()
else:
l.backward()
grad_clipping(net, 1)
# Since the `mean` function has been invoked
updater(batch_size=1)
metric.add(l * y.numel(), y.numel())
return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()equation 8.7.16 seems to be wrong. dh(t)/dWhh != h(t-1), but equal to what’s expressed in equation 8.7.7. same for dh(t)/dWhx.
please correct me if there is some hidden assumption, thanks.
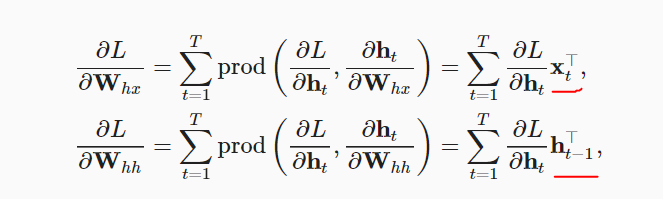
I think it should be an “=” too.
So do I. The first term is same as the second term.
perhaps he is referrind to dL/dw and not partial L / partial w
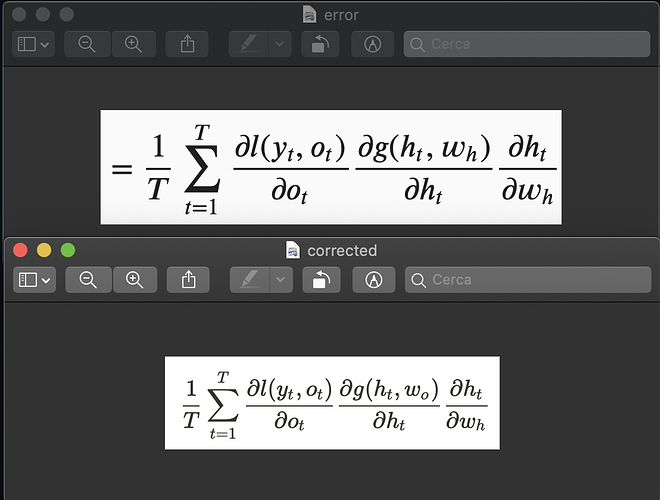
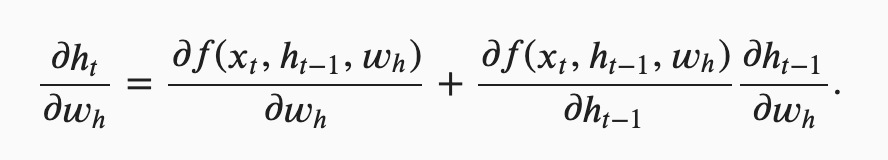
 here?while I think it’s = here.
here?while I think it’s = here.
