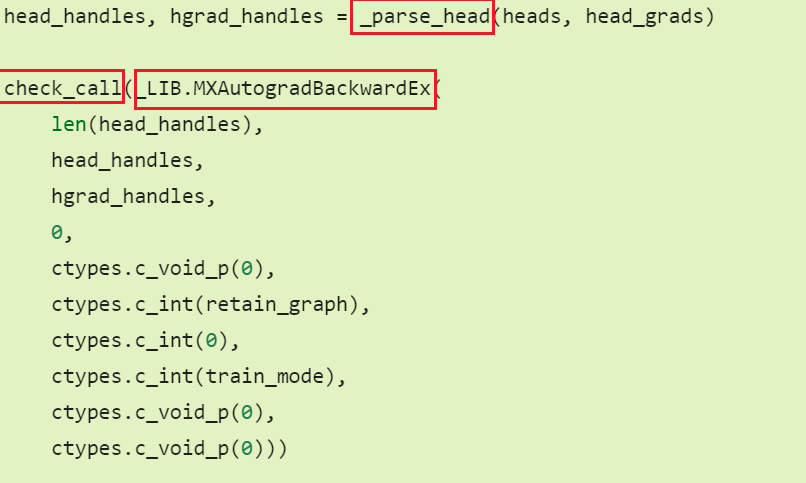
my solution to question 5
import numpy as np
from d2l import torch as d2l
x = np.linspace(- np.pi,np.pi,100)
x = torch.tensor(x, requires_grad=True)
y = torch.sin(x)
for i in range(100):
y[i].backward(retain_graph = True)
d2l.plot(x.detach(),(y.detach(),x.grad),legend = ((âsin(x)â,âgrad w.s.t xâ)))
I think it would be cool if in section 2.5.1 (and further where it occurs) there would be something like this $\frac{d}{dx}[2x^Tx]$.
Any take on this question 
Why is the second derivative much more expensive to compute than the first derivative?
I know second derivatives could be useful to give extra information on critical points found using 1st derivative, but how does 2nd derivatives are expensive ?
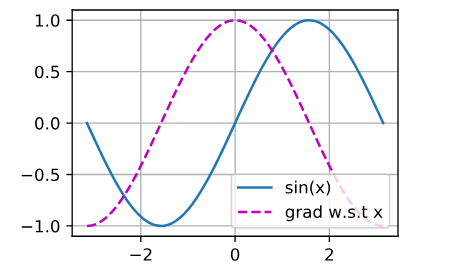
My solution:
from mxnet import np, npx
npx.set_np()
from mxnet import autograd
def f(x):
return np.sin(x)
x = np.linspace(- np.pi,np.pi,100)
x.attach_grad()
with autograd.record():
y = f(x)
y.backward()
d2l.plot(x,(y,x.grad),legend = [('sin(x)','cos(x)')])
@asadalam
You can use 
or a github URLto show codeâŚ
And we should aviod import torch and mxnet at the same timeâŚ
It is confusingâŚ
Any specific reason not to use both torch and mxnet and how can we use the functions like attach_grad() and build a graph without using mxnet and only simple numpy ndarrays?
@asadalam
For your first question, the reason is that in your code, you didnât use anything related to pytorch.
So it is unnecessary to import torch
For your second question,
https://mxnet.apache.org/versions/1.6/api/python/docs/api/autograd/index.html#mxnet.autograd.backward
Check for source code
I donât understand nowâŚ
What does these mean?
@szha
Oh yes, sorry, I initially used torch to use itâs sine function but couldnât integrate with attach_grad and building the graph. Switched to numpy function but forgot to remove import torch 
You can try pytorch code too. It will work.
I did a few examples and discovered a problem:
from mxnet import autograd, np, npx
import math # function exp()
npx.set_np()
x = np.arange(5)
print(x)
def f(a):
# return 2 * a * a # works fine
return math.exp(a) # produces error
print(f(1)) # shows 2.78181...
x.attach_grad()
print(x.grad)
with autograd.record():
fstrich = f(x)
fstrich.backward()
print(x.grad)
works fine with the function 2xx (or other polynoms) but produces error with exp(x)
TypeError: only size-1 arrays can be converted to Python scalars
[0. 1. 2. 3. 4.]
2.718281828459045
[0. 0. 0. 0. 0.]
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-78-cea180af7b0c> in <module>
11 print(x.grad)
12 with autograd.record():
---> 13 fstrich = f(x)
14 fstrich.backward()
15 print(x.grad)
<ipython-input-78-cea180af7b0c> in f(a)
6 def f(a):
7 # return 2 * a * a # works fine
----> 8 return math.exp(a) # produces error
9 print(f(1)) # shows 2.78181...
10 x.attach_grad()
c:\us....e\lib\site-packages\mxnet\numpy\multiarray.py in __float__(self)
791 num_elements = self.size
792 if num_elements != 1:
--> 793 raise TypeError('only size-1 arrays can be converted to Python scalars')
794 return float(self.item())
795
TypeError: only size-1 arrays can be converted to Python scalars
I have no idea, why exp() doesnât work.
Hello,
For the question :
âWhy is the second derivative much more expensive to compute than the first derivative?â
One answer :
This is due to the fact that second derivation lead to compute N² elements from a matrix.
Please check details below.
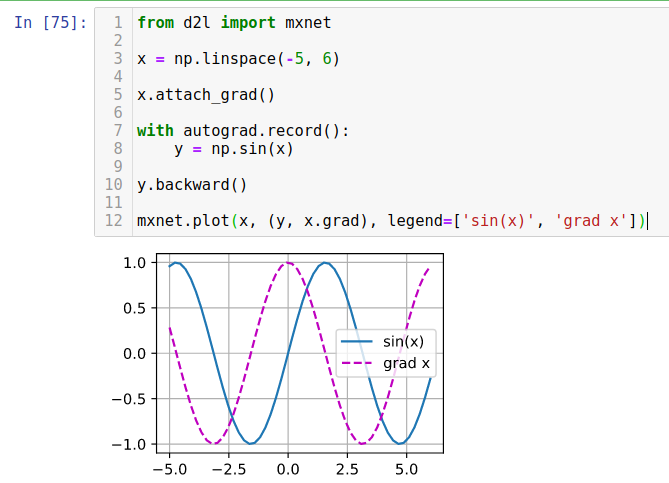
Hello,
Plot sin(x) and derivative of sin(x) without the use of analytic form of the derivative can be achieved without the use of automatic differentiation framework provided by mxnet or pytorch, such as explained below :
The two plots lead to the follwings graphics :
I really dont understand Automatic Differentiation. Up until this topic, everything was intuitive and understanding for me. But i am kind of stuck here. Can i get a detailed explanation what Automatic DIfferentiation is used for. And the code is also not clear for me.
Automatic differentiation allows :
- to automaticaly calculate the derivative of a function and
- apply the resulted function to a given data.
E.g, suppose you use F(x) = 2sin(3x)* and you want to get the derivative of F for the value (array form) A=[1.,12.]
For doing so, you manually you calculate Fâ(x) = 6cos(3x) and then you apply value of A to the derivative, leading to [6cos(3), 6cos(36)]
Automatic differentiation avoid you to implement and calculate Fâ(A).
Just attaching the operator gradient to the x variable, with instruction x.attach_grad(), automatically triggers derivative operations as described just above :
- the calculation of derivative Fâ(x) = 6cos(3x) and
- the calculation of the value of A for this derivative : Fâ([1.,12.]) = [6cos(3), 6cos(36)]
This considerably ease the implementation of code with derivative operations, such as in back propagation.
Exercise 5 in Tensorflow
import math
import numpy as np
x = tf.range(-3,3,0.1)
y = np.sin(x)
d2l.plt.plot(x,y)
# gradient
with tf.GradientTape() as t:
t.watch(x)
p = tf.math.sin(x)
d2l.plt.plot(x,(t.gradient(p,x)))
