https://d2l.ai/chapter_attention-mechanisms-and-transformers/attention-pooling.html
HI,
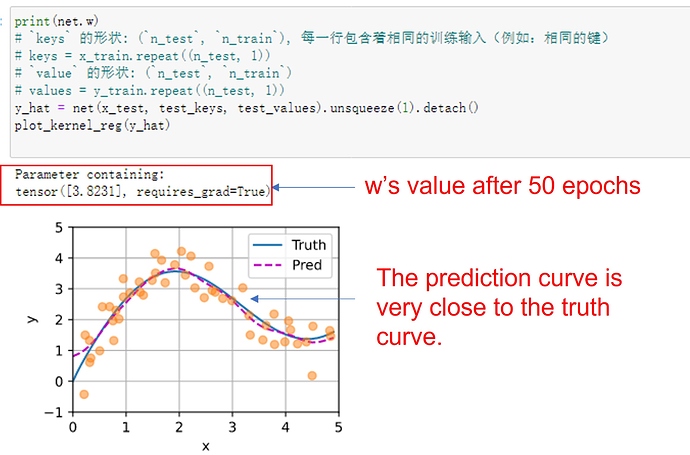
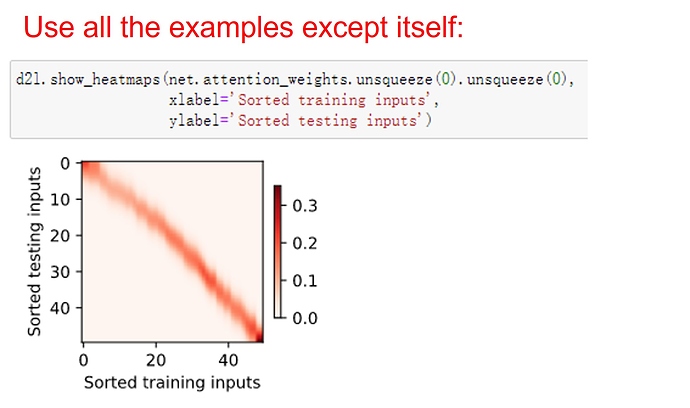
- In the parametric attention pooling, any training input takes key-value pairs from all the training examples except for itself to predict its output.-
I don’t know why can’t we use itself to predict its output. Is it because that the output of the softmax is too large, i.e. the weight of its value is large, so that the rest of the training set are relatively useless?
My take: the parametric version is an optimization problem to find the correct function while the non-parametric version has a function already.
Since it’s an optimization problem, the loss we optimize is based on the training examples (the error in the estimation over all the training examples). We could achieve zero loss if the gaussian kernel’s width w becomes tiny i.e. it only weights the training output at the current input and disregards everything else. There is nothing wrong inherently with that but the resulting estimator is literally just a set of points (it estimates exactly the y_i at a particular training x_i) with a width w -> 0. This leads to a straight line i.e. the “dumb” averaging estimator.
I am not sure I understand correctly, but wouldn’t in the case of x=x_i result in
sofmax(-1/2((x_i-x_i)*w)^2)
In which case the respective i_th prod would be zero?
Because x itself (key) does not have a label y (value): we are predicting its y
Inverse Kernel (Lenrek?)
Question 4 lead me onto a kernel potentially useful for the inverse purpose of most attention kernels.
Kernel:
self.attention_weights = (
torch.abs((queries-keys)*self.w)
/torch.sum(torch.abs((queries - keys)*self.w), dim=(0))
)
Effect:
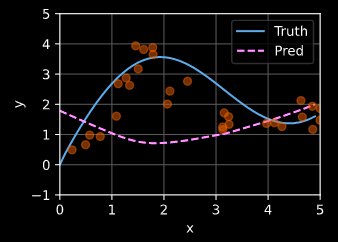
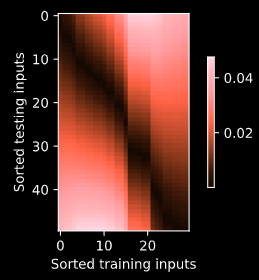
Description:
Does the opposite of what attention weights normally do:
Shifts focus AWAY from the closest neighbors.
Potentially useful for components focusing on long-range dependencies.
If you find it useful, please call this kerneL ‘Lenrek’.
in Exercises 4:
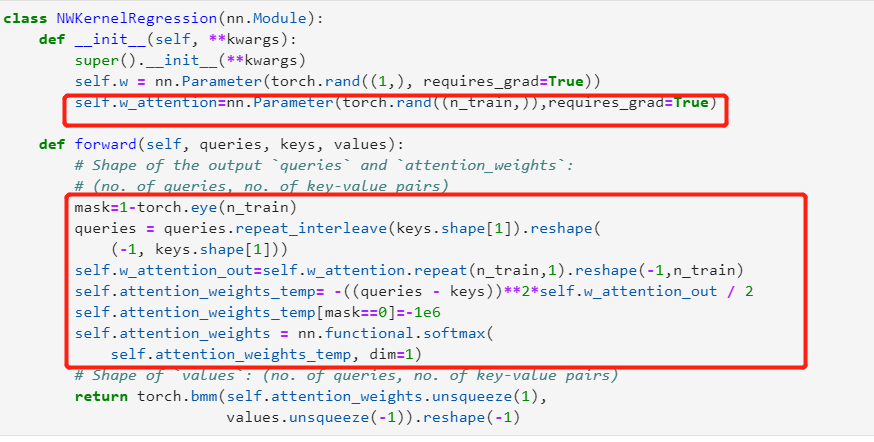
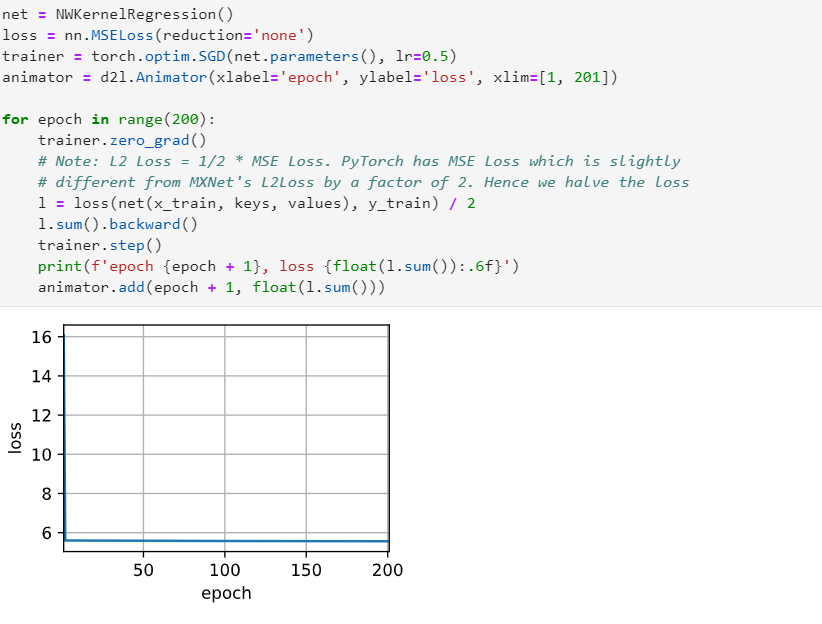
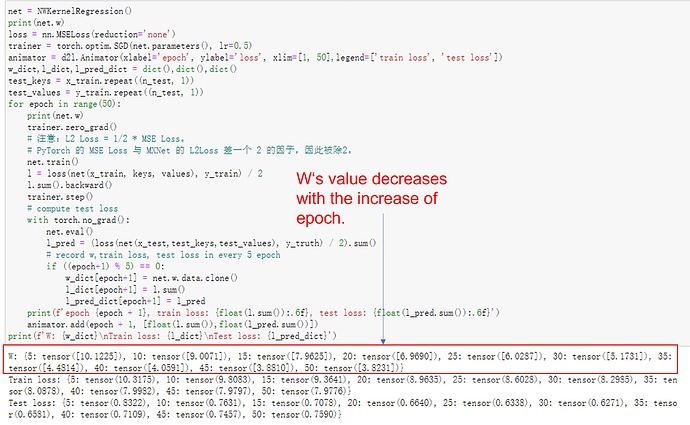
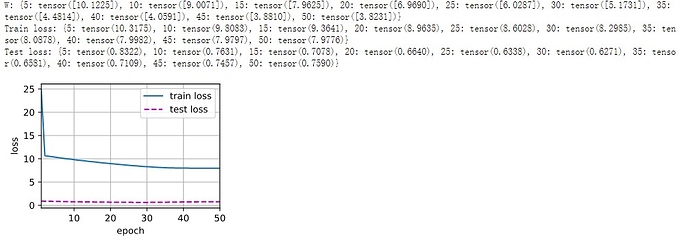
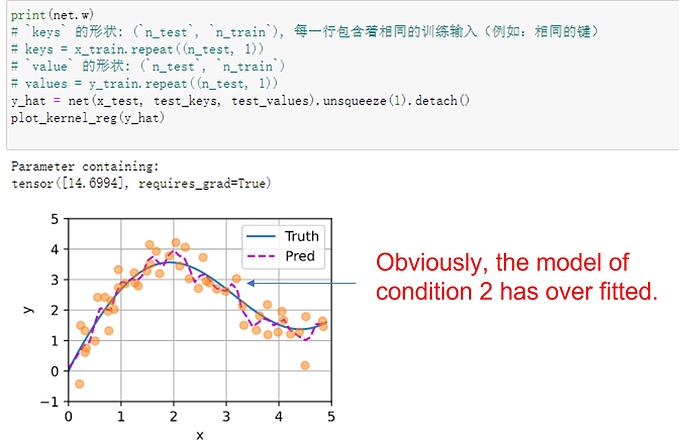
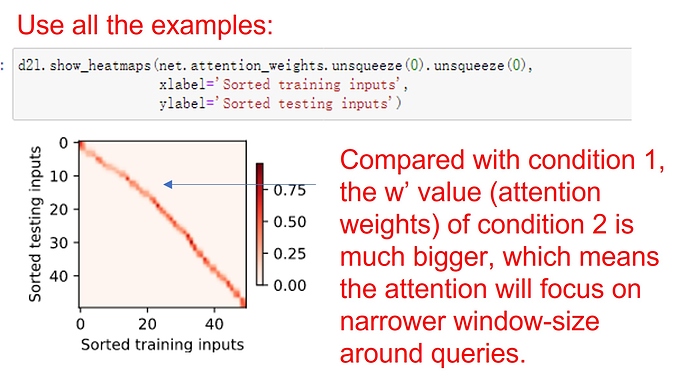
add a attention layer and a mask layer to the attention weight. when trainning the loss smmoth than before.
trainning the model in the paper 200 epoch i think maybe it go into a local minmum
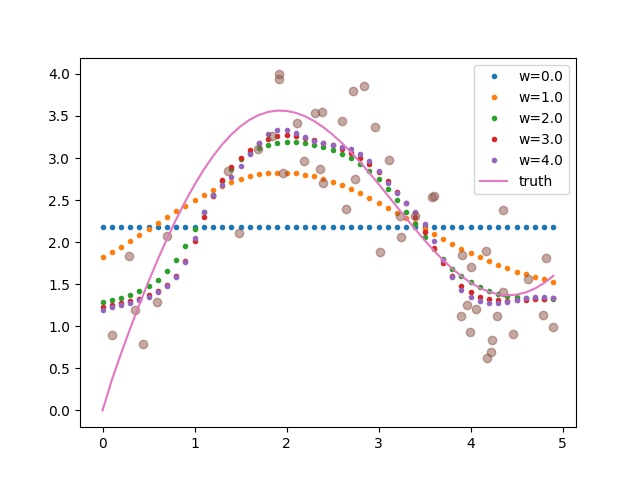
Having the learnable parameter w multiplying the distance between x and x_i after the squaring rather than before in the forward function seems to be smoother and less prone to overfitting, thus produces more desirable results :
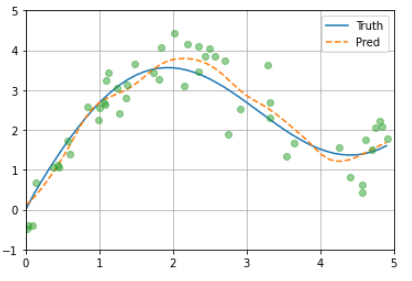
What is the reasoning behind this behavior?
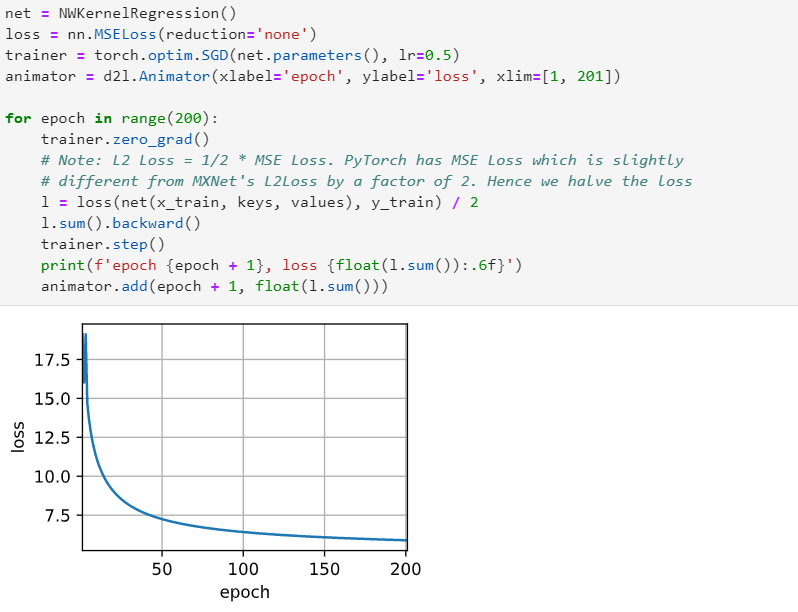
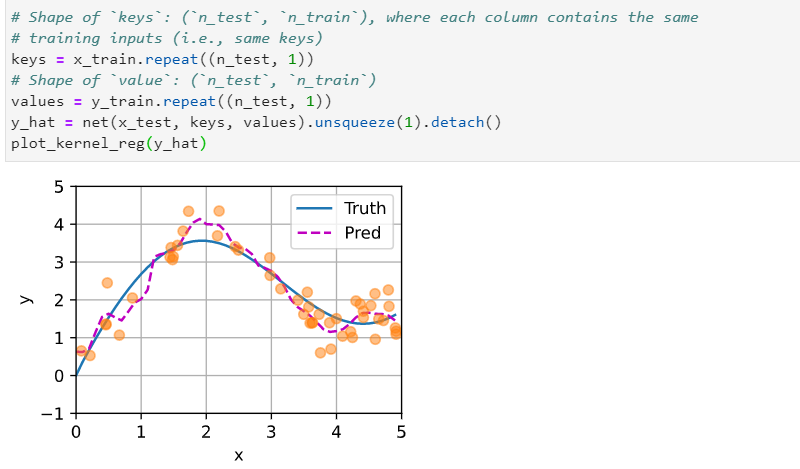
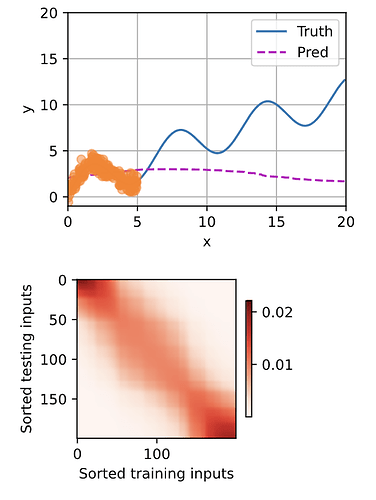
Q1: 1. Increase the number of training examples. Can you learn nonparametric Nadaraya-Watson kernel regression better?
With using 200 training and 200 testing examples, I found the performance of nonparametric Nadaraya-Watson kernel regression decreases with the increasing number of examples
Hi, for Nadarya-Watson Kernel regression, is it necessary that the inputs (X) are unidimensional? Can X_train be of the shape (n_train, d) where d > 1? If so how would we proceed with the problem.
@Raj_Sangani For d >= 1, you can define a distance function, e.g., Minkowski distance:
dist(x, z; p) = (x - z).abs().pow(p).sum().pow(1/p)
I tried to develop an understanding of attention mechanism through this course and it was helpful but I am unable to understand and do exercises. Please give me suggestions to develop my understanding
Regression is a good one offering the sense of scoring attentions.
But how makes them relative to the query, key and value mechanism?
I decided to make them act in that way, hope it’s helpful.
def gaussian_with_width(x, sigma):
return torch.exp(-x**2 / (2*sigma**2))
def f(x):
return 2 * torch.sin(x) + x
n = 8
#### init
noise = torch.rand(n)
x1, _ = torch.sort(torch.rand(n) * 4)
y1 = f(x1) + noise
x2 = torch.arange(x1[0]-1, x1[-1]+1, 0.5)
y2 = f(x2)
d = x2.reshape((-1, 1)) - x1.reshape((1, -1))
#### original less distance, more attention
kr = gaussian_with_width(d, 0.1).type(torch.float32)
kr_norm = (kr.T/kr.sum(1)).T
w1 = kr_norm # score nq x nk
print("check layer norm:", kr_norm.sum(1))
# what if qkv
k = y1.reshape(-1,1) # key nk x d=1
q = y2.reshape(-1,1) # query nq x d=1
v = y1.reshape(-1,1) # value nk x nv=1
#### kernel must be made of query and key
w2 = q@k.T
w2 = nn.functional.softmax(w2,dim=-1)
w = w2
y = w@v # value nq x nv
#### display
fig, ax = plt.subplots(figsize=(8,4))
plt.plot(x1, k.flatten(), 'o-')
plt.plot(x2, q.flatten(), 'x-')
plt.plot(x1, v.flatten(), '.')
plt.plot(x2, y.flatten(), '.-')
ax.legend(['k', 'q', 'v', 'y'])
plt.show()
fig.canvas.manager.set_window_title("qkv")