前向传播、反向传播和计算图

[xiaotinghe]

http://zh.d2l.ai/chapter_multilayer-perceptrons/backprop.html

[d2l-Commentor]

为啥这一章没人讨论呀， ____________________________________

[wu_zheng]

这一小节中的计算图、反向传播等内容在视频课程中有介绍么

[Sandra]

没有单独视频————————————————

[HeartSea15]

#######################################

1. 矩阵乘法不满足交换律，怎么这里放在前面了？
   
   

[Sandra]

因为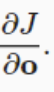 是个向量。向量@矩阵 和 矩阵转置@向量 的结果都是一样的，都是一个向量

[Fox]

这一章的一些想法，剩下的放知乎里了

[mtfelix]

请问在计算图中，一个变量x(方框)只能输入给(指向)唯一一个操作符(圆圈)是吧？ 否则x.grad需要存储多个操作符对应的累积导数吧？

比如:
x->f1
x->f2

f1.backward()
f2.backward()

then, what is x.grad?

[ZL_CHEN]

视频在哪里观看啊，评论区能放个链接嘛，z s b d

[HJX]

书上有说，这个主要是因为prod运算符是指执行必要的操作，也就是说会自动根据需要进行换位和交换输入位置等，然后再进行相乘

[Jin_Zhou]

这个计算图非常重要，也是基础的基础，理解了计算图就理解了求梯度并更新的所有代码，强烈建议自己写个线性回归走一遍pytorch的计算图流程

[saiku]

b站搜李沐老师就能找到了（为什么要写满20个字才能发 ）

[Yang_Tim]

不对吧，假设向量的shape是(1,4)，矩阵的shape是(4,3)，向量@矩阵是(1,4)(4,3)=(1,3)，而矩阵转置@向量是(3,4)(1,4)无法进行矩阵运算的

[leebyee]

预测应该不需要这么多吧，我理解只存储当前层的输入输出是不就够了？不用保存前面层的信息，比如计算完h后，z的内存就可以释放掉了。

[Fopdoodle]

x.grad会累加的，所以一般每次迭代都会调用torch.grad.zero_()清除之前的导数

[tx2002]

这章对初学者不太友好，鱼书的这部分会好懂很多

[hedong_gong]

这章对权重矩阵L2范数的梯度计算好像有点问题，对平方和开根号的式子求导应该更复杂些

[HelloWorldU]

向量乘以矩阵的偏导就是矩阵的转置乘以向量啊

[LyricsGo]

因为用的是L2范数的平方（没有根号）

[LyricsGo]

原文
Besides, the size of such intermediate values is roughly proportional to the number of
network layers and the batch size.
大小→规模