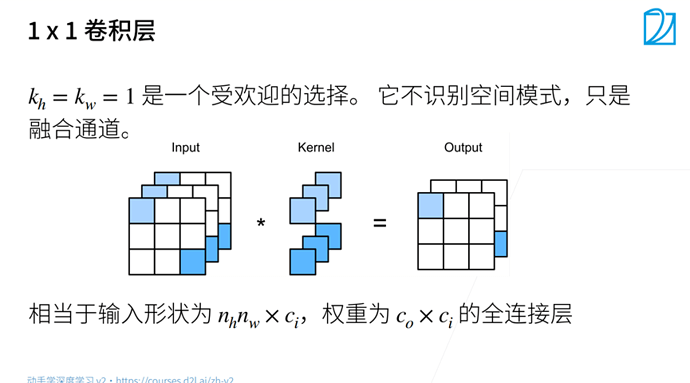
https://zh.d2l.ai/chapter_convolutional-neural-networks/channels.html
本节课程的练习6.5.4
请问应该如何计算“计算成本computational cost”和“内存占用memory footprint”?我没有在前序的课程中找到相关的知识介绍,希望得到解答,非常感谢。
针对你的问题,我的看法是这样的:
1、卷积操作看成是提取特征的方式,卷积核神经元就是图像处理中的滤波器,卷积层的每个滤波器都会有自己所关注一个图像特征,比如垂直边缘,水平边缘,颜色,纹理等等,这些所有神经元加起来就好比就是整张图像的特征提取器集合。这种提取特征方式与位置无关(就如why-conv里说的平移不变性:不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”)。个人理解这种不变性是基于物理实际的,即相同的特征模式对应于一种物理实际,比如物体间的边缘界面理论上是可以通过空间图像的差异区分(体现在图像颜色上就是色差值和色差梯度等这些指标,当然前提是图像有足够高的锐度),那么这种提取后的特征也应该适用于图像的其它部分。所以对图像的各个输入,单个二维卷积张量,也就是文中的一个Kh*kw矩阵是权值共享的,偏置项也是如此。
2、针对“每个卷积核里的每个参数共用一个偏差吗”,我觉得是的,共用一个偏置bias(你说的偏差)即可。因为互相关运算对偏置项是求和运算,即使你给每个参数设置不同的偏置值,最终这些偏差求和后也只会得到一个偏置值。而之所以能对图像不同部分应用同一个偏置值,原因是上面第一条。
3、你说的“感觉和多层感知机里的每个输入都有独立的偏差不太一样”的说法应该不对。偏置bias(你说的偏差)是针对输出而言的,不是针对输入,偏置项的维度跟输出项的维度是一样的,而不是跟输入项,不是“每个输入都有独立的偏差",而是每个输出维度都有独立的偏差(当然很多时候,bias初始值在各个维度上的值都设为一样)。
6.4.5 练习
-
没理解题意,不懂两个卷积核的结构是什么样的。。。
-
2.1 ⌊(𝑛ℎ−𝑘ℎ+𝑝ℎ+𝑠ℎ)/𝑠ℎ⌋×⌊(𝑛𝑤−𝑘𝑤+𝑝𝑤+𝑠𝑤)/𝑠𝑤⌋×ci×co
2.2 ci×h×w+co×ci×kh×kw+co×⌊(𝑛ℎ−𝑘ℎ+𝑝ℎ+𝑠ℎ)/𝑠ℎ⌋×⌊(𝑛𝑤−𝑘𝑤+𝑝𝑤+𝑠𝑤)/𝑠𝑤⌋
2.3 co×ci×kh×kw
2.4 ⌈kℎ/sℎ⌉×⌈kw/sw⌉×co×ci×kh×kw -
4倍。增加(ph×pw)/(sh×sw)×ci×co的计算数量
-
h×w×ci×co
-
因为输入的X和K是浮点数,后续浮点数计算会有误差
def corr2d_matmul(X, K): #@save
"""计算二维互相关运算。"""
h, w = K.shape
yh, yw = (X.shape[0] - h + 1, X.shape[1] - w + 1)
K = K.reshape((h * w, 1))
Y = []
for i in range(yh):
for j in range(yw):
Y.append(X[i:i + h, j:j + w].reshape(h * w))
Y = torch.stack(Y, 0)
Y = torch.matmul(Y, K).reshape(yh, yw)
return Y
def corr2d_multi_in_matmul(X, K):
# 先遍历 “X” 和 “K” 的第0个维度(通道维度),再把它们加在一起
return sum(corr2d_matmul(x, k) for x, k in zip(X, K))
def corr2d_multi_in_out_matmul(X, K):
# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。
# 最后将所有结果都叠加在一起
return torch.stack([corr2d_multi_in_matmul(X, k) for k in K], 0)
4.1.2,维度为(k1H+K2H-1)X(K1W+K2W-1)
4.1.3,反之不一定
请问内存占用和计算成本是怎么算的








请问,为什么多通道卷积是把不同通道的结果简单相加呢,这样做的意义是什么呢?
谢谢
2.1 计算成本:
1.kernel 每次滑动要进行kh * kw次乘积运算以及kh * kw - 1次加法运算. 一共有ci层所以是ci * kh * kw + ci * kh * kw - 1
2.输出图像尺寸(h-kh+2ph)/sh + 1以及(w-kw+2pw)/sw + 1
3.一共co个核,计算成本为(ci * kh * kw + ci * kh * kw - 1) * ((h-kh+2ph)/sh + 1) * ((h-kh+2ph)/sh + 1) * co
- 应该是要证明两个较小的卷积层能够使用一个较大的卷积层来代替。
1.1 证明的话通过最后感受野的大小一致可以推导出来。
1.2 步长为1,padding为0的时候,等效的大小是(k1+k2-1)
1.3 反之应该也可以。 - 假设单通道最后输出的维度是mh和mw
2.1 单通道卷积核计算一次出进行kh * kw次乘法以及kh * kw - 1次加法,需要遍历mh * mw次。多个输入通道之间需要相加,一共是mh * mw * (ci - 1)次。所以最后计算成本是 co * [(mh * mw) * (kh * kw * 2 -1) + mh * mw * (ci - 1)]
2.2 内存包括输入、输出、卷积核的大小(没有算梯度的)。ci×h×w+co×ci×kh×kw+co×mh×mw。
可以理解成加权相加。是对多个上层输出通道识别出来的patten的一个聚合。只是这里的加权值是可以融合到卷积核里的。
我认为bias的维度应该是Co,pytorch的代码也验证了我的想法

Q1: 假设我们有两个卷积核,大小分别为k_1和k_2(中间没有非线性激活函数)。
1. 证明运算可以用单次卷积来表示。
答:参见Google的Inception v3的论文:Rethinking the Inception Architecture for Computer Vision
2. 这个等效的单个卷积核的维数是多少呢?
答:假设这两个卷积核不是1×1卷积核,且stride=1, padding=0,则可得该等效的单个卷积核的维数k = k_1 + k_2 - 1(如果卷积核k_h和k_w不同,则分别计算)。
3. 反之亦然吗?
答:反之亦然,即单个卷积核也可以用两个卷积核等价表示(此时1×1卷积核也成立)。
Q2: 假设输入为c_i×h×w,卷积核大小为c_o×c_i×k_h×k_w,填充为(p_h, p_w),步幅为(s_h, s_w)。
1. 前向传播的计算成本(乘法和加法)是多少?
答:c_o×c_i×(⌊(ℎ−𝑘_ℎ+𝑝_ℎ+𝑠_ℎ)/𝑠_ℎ⌋×⌊(𝑤−𝑘_𝑤+𝑝_𝑤+𝑠_𝑤)/𝑠_𝑤⌋)×(k_h×k_w + k_h×k_w-1)。
2. 内存占用是多少?(是指参数所占的内存?还是指参数以及数据的内存占用?)
答:前者:c_i×h×w+c_o×c_i×k_h×k_w+c_o×⌊(ℎ−𝑘_ℎ+𝑝_ℎ+𝑠_ℎ)/𝑠_ℎ⌋×⌊(𝑤−𝑘_𝑤+𝑝_𝑤+𝑠_𝑤)/𝑠_𝑤⌋
3. 反向传播的内存占用是多少?
答:不会算
4. 反向传播的计算成本是多少?
答:不会算
Q3: 如果我们将输入通道c_i和输出通道c_o的数量加倍,计算数量会增加多少?如果我们把填充数量翻一番会怎么样?
A3: 如果输入通道c_i和输出通道c_o的数量加倍,则计算量变为原来的4倍;如果填充数量翻一番,则计算量增加c_o×c_i×(p_w/s_w)×(p_h/s_h)。
Q4: 如果卷积核的高度k_h=k_w=1和宽度是,前向传播的计算复杂度是多少?
A4: c_o×(2×c_i-1)×(h×w)
Q5: 本节最后一个示例中的变量Y1和Y2是否完全相同?为什么?
A5: 因为浮点数计算有误差,所以两者不完全相同,这个我在6.1底下的reply已经通过代码验证过,详情请看https://zh.d2l.ai/chapter_convolutional-neural-networks/why-conv.html
Q6: 当卷积窗口不是1×1时,如何使用矩阵乘法实现卷积?
A6:
def corr2d_multi(X, K):
h, w = K.shape
outh = X.shape[0] - h + 1
outw = X.shape[1] - w + 1
K = K.reshape(-1, 1)
Y = []
for i in range(outh):
for j in range(outw):
Y.append(X[i:i + h, j:j + w].reshape(-1))
# 这个完全没想到,感谢@thirty
Y = torch.stack(Y, 0)
# 用矩阵乘法表示互相关运算
res = (torch.matmul(Y, K)).reshape(outh, outw)
return res
def corr2d_multi_in(X, K):
"""多输入通道"""
# 先遍历“X”和“K”的第0个维度(通道维度),再把它们加在一起
# return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
return sum(corr2d_multi(x, k) for x, k in zip(X, K))
def corr2d_multi_in_out(X, K):
"""多输出通道"""
# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。
# 最后将所有结果都叠加在一起
# return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
def conv2d_mm(x,k):
'''使用im2col方式计算,没有考虑batch size'''
#计算输出的尺寸
h, w = k.shape[-2], k.shape[-1]
outh = x.shape[-2] - k.shape[-2] + 1
outw = x.shape[-1] - k.shape[-1] + 1
#摘取数据
tmpx = []
for i in range(outh):
for j in range(outw):
tmpx.append(x[:,i:i+h, j:j+w].reshape(-1,1))
#把摘取的数据堆叠为矩阵,每一列为相应位置摘取的所有通道的数据,用来与卷积核做矩阵乘法
#使用torch.cat()和torch.stack()都可以
tmpx = torch.cat(tmpx, 1)
#tmpx = torch.stack(tmpx, 1).squeeze()
#卷积核变为行向量,每一行是一个卷积核的参数,共有c_o行
k = k.reshape(k.shape[0], -1)
#把结果reshape为c_0 X outh X outw形状
y=torch.mm(k, tmpx).reshape(k.shape[0], outh, outw)
return y
- 请问一下Q2第一问可以写一下推导过程么(答案都可以稍微写下推导过程,方便我们理解你的思路并验证),比如乘法计算量为
c_o×c_i×(⌊(ℎ−𝑘_ℎ+𝑝_ℎ+𝑠_ℎ)/𝑠_ℎ⌋×⌊(𝑤−𝑘_𝑤+𝑝_𝑤+𝑠_𝑤)/𝑠_𝑤⌋)×(k_h×k_w)
加法计算量为(我理解是因为你考虑到n个数只要相加n-1次)
c_o×c_i×(⌊(ℎ−𝑘_ℎ+𝑝_ℎ+𝑠_ℎ)/𝑠_ℎ⌋×⌊(𝑤−𝑘_𝑤+𝑝_𝑤+𝑠_𝑤)/𝑠_𝑤⌋)×(k_h×k_w-1)
在李沐老师的B站视频中,算法复杂度好像可以直接用O(Ci * Co * Kh * Kw * Mh * Mw)
其中
输入x: Ci * Nh * Nw
核W: Co * Ci * Kh * Kw
偏差B: Co * Ci
输出Y: Co * Mh * Mw
我理解就算是按照你的结果,化简一下就是
c_o×c_i×(⌊(ℎ−𝑘_ℎ+𝑝_ℎ+𝑠_ℎ)/𝑠_ℎ⌋×⌊(𝑤−𝑘_𝑤+𝑝_𝑤+𝑠_𝑤)/𝑠_𝑤⌋)×(2×k_h×2×k_w-1)
在计算复杂度表达中,可以省去常数项,应该也可以表示为
c_o×c_i×(⌊(ℎ−𝑘_ℎ+𝑝_ℎ+𝑠_ℎ)/𝑠_ℎ⌋×⌊(𝑤−𝑘_𝑤+𝑝_𝑤+𝑠_𝑤)/𝑠_𝑤⌋)×(k_h×k_w)
同李沐老师给出的公式
如果有任何错误,请指正
2.Q3的A3中,填充数量翻一番,计算量增加是怎么计算的呢?
我这边参照前一章的公式6.3.1:
$$ (n_h-k_h+p_h+1)\times(n_w-k_w+p_w+1) $$
将Ph和Pw变成2Ph,2Pw和原式相减,结果为Pn*(Nw-Kw+2Pw+1)+Pw*(Nh-Kh+2Ph+1)
我理解这个是输出维度大小增量,套入李沐老师视频说的时间复杂度O(Ci * Co * Kh * Kw * Mh * Mw)
我觉得增量应该为(Pn*(Nw-Kw+2Pw+1)+Pw*(Nh-Kh+2Ph+1)) * Ci * Co * Kh * Kw
- Q6我想补充一点细节,之前我看到这个代码是懵的,因为没有示例不够直观,我添加了一些示例和代码注释,应该可以帮到和我一样有类似困惑的人,代码如下:
def corr2d_multi(X,K):
h,w=K.shape
outh=X.shape[0]-h+1
outw=X.shape[1]-w+1
K=K.reshape(-1,1)
Y=[]
for i in range(outh):
for j in range(outw):
Y.append(X[i:i+h,j:j+w].reshape(-1))#将需要计算的局部矩阵拉伸成一个向量并纳入Y
Y=torch.stack(Y,0)
res=torch.matmul(Y,K).reshape(outh,outw)
return res
def corr2d_multi_in(X, K):
# 先遍历“X”和“K”的第0个维度(通道维度),再把它们加在一起
return sum(corr2d_multi(x, k) for x, k in zip(X, K))
def corr2d_multi_in_out(X, K):
# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。
# 最后将所有结果都叠加在一起
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
K = torch.stack((K, K + 1, K + 2), 0)
print(X.shape)#torch.Size([2, 3, 3])
print(K.shape)#torch.Size([3, 2, 2, 2])
print(corr2d_multi_in_out(X, K).shape)#torch.Size([3, 2, 2])
#上面的输出中3=K.shape[0],[2,2]为输出层大小,具体计算公式为上一章的6.3.1,Xh-Kh+1=3-2+1=2,w同理
1.a 这个题目有点坑,应该是两个卷积核,一个在前,一个在后,而不是并行,那么最后的feature map大小为:
n-K1+1-K2+1=n-(K1+K2-1)+1
等于进行了一次单次卷积,卷积核大小为K1+K2-1
1.b 卷积核大小为K1+K2-1
1.c 同样的,一个卷积核也可以逆过来使用两个卷积核进行替换,如一个55可以替换成两个33