https://zh.d2l.ai/chapter_multilayer-perceptrons/environment.html
上述算法依赖于一个重要的假设： 需要目标分布(例如，测试分布)中的每个数据样本在训练时出现的概率非零。请问这里应该怎么理解？
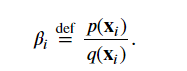
我觉得是这个公式决定的吧，要不然重要性权重就变成无穷大了
1 Like
标签偏移那，混淆矩阵C是怎么得到的啊？没看明白
正如我们向他们解释的那样，用近乎完美的精度来区分健康和患病人群确实很容易。 然而，这是可能因为受试者在年龄、激素水平、体力活动、 饮食、饮酒以及其他许多与疾病无关的因素上存在差异。 这对检测疾病的分类器可能并不适用。 这些抽样可能会遇到极端的协变量偏移。
区分容易是因为无关因素有差异吗？不应该是无关因素差异越小越容易区分吗？另外抽样遇到协变量偏移是相对于什么而言的？是因为大学生的特征相对于一般健康男性发生了偏移吗？还是说用大学生作为健康样本训练出来的模型，用在测试所有其他病人时会遇到协变量偏移的情况。
意思是说区分正负样本容易，因为正负样本在一些无关变量上差异很大。但是这些变量实际上和疾病预测无关，对预测疾病没有帮助。模型只是区分了年轻人和老年人而不是健康人和患者。
2 Likes
第二题是不是构建一个二分类，训练后得到的函数是h(x)，若对于任意的x来源于训练集都有h(x)=0，那么就没有偏移，反之则发生了偏移
看下我和gpt的对话
Q: 也就是说，只有血液特征，没有年龄、激素水平、体力活动、饮食、饮酒等数据特征，训练出来的分类器可以很准确的区分病人和健康人，但是如果用来实际预测的化，效果很容易被干扰。
比如一个饮酒的健康人，可能血液样本会类似病人？
A:是的，您理解得非常正确。
在这个例子中，我们假设仅使用血液特征进行训练，并且没有考虑其他与疾病无关的因素。在这种情况下，分类器可能会在训练数据上表现出很高的准确度，能够很好地区分病人和健康人。
然而，在实际应用中，存在多种与疾病无关的因素，如年龄、激素水平、体力活动、饮食、饮酒等。这些因素可能会对血液样本产生影响，使得一些健康人的血液样本与患病人的血液样本相似，从而干扰了分类器的准确性。
比如，如果一个健康人长期饮酒，那么他的血液样本可能会反映出某种异常，类似于患病人的血液样本。这样，即使他是健康的，分类器也可能错误地将他归类为患病人。
因此，为了提高分类器的准确性和适用性，我们需要综合考虑多个因素，并引入更多相关的特征，而不仅仅依赖于血液特征。这样可以更好地对疾病进行预测和诊断，减少由于其他因素引起的误判。
第二题提示说构造一个分类器来实现协变量偏移检测器，常规思路可能就是用源分布来训练分类器，再在目标分布上进行测试，根据测试集上预测结果和实际标签的吻合情况来判断。可是这样怎么区分是协变量偏移还是分类器过拟合呢，还是说有更好的思路？还望各位大佬不吝赐教QwQ
感觉这一章节的内容翻译得很不好，语句都不通顺也缺乏逻辑，我怀疑是不是用机器翻译的
1 Like
文中说了不能计算目标数据集的混淆矩阵C，计算的是源数据集的C，假设是一个很强的假设，( P(X|Y) ) 相同，说明了计算出来的比例是一样的，也就是C是一样的。直接说使用源的混淆矩阵也是可行的。
gpt4 回答的：
混淆矩阵 ( C ) 中的元素 ( C_{ij} ) 表示实际类别为 ( i ) 被预测为类别 ( j ) 的概率。因此，如果 ( P(X|Y) ) 上没有差异，那么预测错误的模式和错误概率在两个数据集之间应该是相似的。换句话说，混淆矩阵反映了特定标签下模型预测表现的内在属性，与标签的全局分布无关。
- 保证特征分布相同的假设：这一点至关重要。如果假设不成立，使用源数据集的混淆矩阵可能会引入误差。
- 样本量足够：源数据集中的每个类别应有足够的样本量来确保统计上的可靠性，特别是混淆矩阵的准确估计。
- 模型泛化性：源数据集上训练出的模型应在目标数据集上有良好的泛化性能。如果模型在源数据集上过拟合，其混淆矩阵可能不适用于目标数据集。
请问本章有英文版本吗？中文翻译版感觉有一些难以理解。
这一节好晕啊，特别从分布偏移纠正开始 
这一节写得不太好，至少翻译得很烂。
在这里，我为包括这一节在内往前的每一节都做了笔记。希望对社区有用。
这一节基本都是迁移学习领域的内容，可以看看《迁移学习导论》详细了解一下
The overall of y hat, which is the mean of y hat in 4.9.10,
is the joint probability that the prediction = i and y actually is j.
The joint probability is the multiplication of condition probability P(y hat=i, y=j)
and event probability P(y=j).
So, Confusion matric “C” is that condition probability matrix.
C[i, j] represents prediction saying y hat = i in the condition y actually is j.