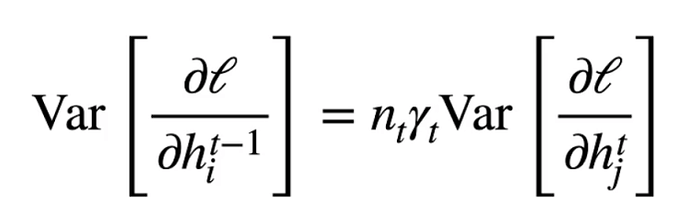https://zh.d2l.ai/chapter_multilayer-perceptrons/numerical-stability-and-init.html
排列对称性那儿没看懂， 进行重排列是什么意思。有相关资料么?
按照我的理解，这句话的意思是指隐藏单元进行排列组合，改变相对位置。但是由于隐藏单元的权重相同，这几次的排列组合计算结果是相同的，因此，只需一个隐藏单元便可代替，从而论证了我们必须要打破对称性才能进行多个单元的有效利用。
2 Likes
我想起来之前，线性函数的层，叠加后仍然可以用一个线性函数代替，所以引入激活函数来增添非线性。这样的思想似乎有一点相通之处
2 Likes
您好！老师，想请教下 “ 不幸的是，上面的问题更为严重： 最初，矩阵 M(l)M(l) 可能具有各种各样的特征值” 如何理解此处的特征值与矩阵求导之后相乘的关系。 
这里不是矩阵求导相乘，而是把求导后的定义为矩阵M，（见4.8.2上的def）。
所以4.8.2相当于一堆矩阵最后乘了一个向量。
我理解的是当开始反向传播的时候，第一层就变成了n_{out}，因为运算流程类似，也有无法收敛的问题，用对输入层同样的公式证明，需要吧int换成out，n_{out}*sigma**2=1才能保持方差稳定，个人理解，欢迎纠正。
1 Like
i和j，，为什么前向传播那块用上一层j的方差得到了下一层i的方差啊。i和j到底那个维度是该看出随机变量啊
可以先画一个计算图，文中描写的公式是n_in个输入的情况下，单独的一个o_i的方差结果应该是什么，这是正向的传播过程，那么对于反向传播，现在假设有n_out个输出（即n_out个o_i）那么对于单独的一个输入（假设是x_i）的梯度的方差，可以想象一下，把之前的n_in个输入替换为n_out个输出，把o_i替换为x_i（也就是把计算图中的数据替换一下），最后梯度的方差的结果很自然的就可以将n_in改写为n_out了