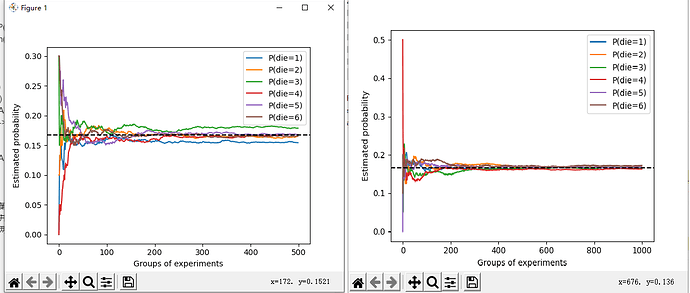
Exercise 1
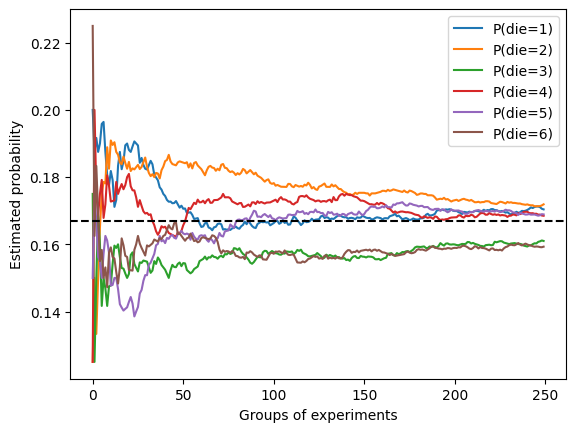
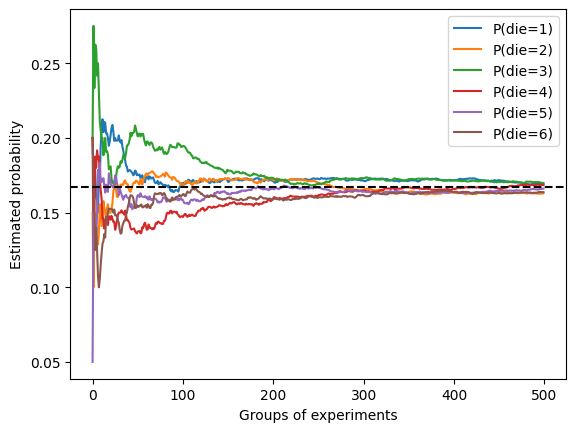
进行500组实验,每组抽取10个样本(左),和进行1000组实验,每组抽取10个样本(右)
可以看出在样本量相同的情况下,进行的实验组数越多,结果越接近真实概率。
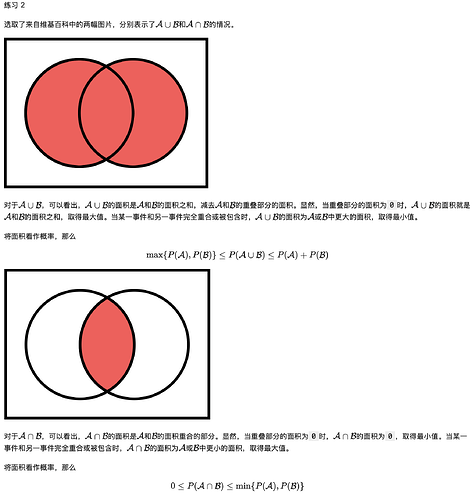
Exercise 2
max(P(A), P(B)) <= P(A ∪ B) <= P(A) + P(B)
0 <= P(A ∩ B) <= min(P(A), P(B))
Exercise 3
P(AB) = P(B | A)P(A)
P(BC) = P(C | B)P(B)
P(ABC) = P(A)P(B | A)P(C | AB)
根据马尔可夫链:(A->B->C)
P(C | AB) = P(C | B)
所以:
P(ABC) = P(A)P(B | A)P(C | B)
第二题
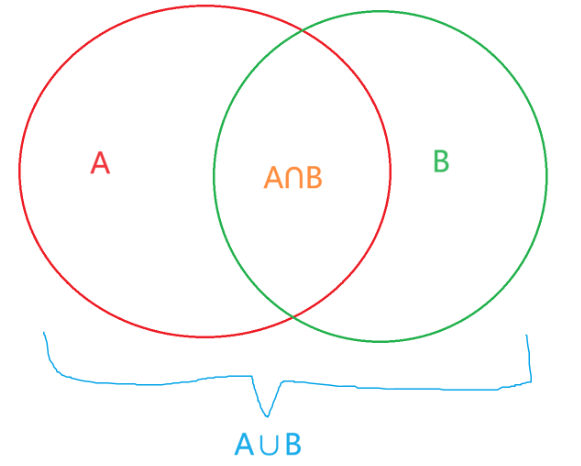
第四题:
不连续使用第一种测试的原因是,保持两次测试的独立性。
假设第二次测试仍然使用测试1,由于重复执行同样的操作,结果相同的概率是客观存在的,那么就需要引入P(D1-2=1|D1-1=1)来继续后续计算。
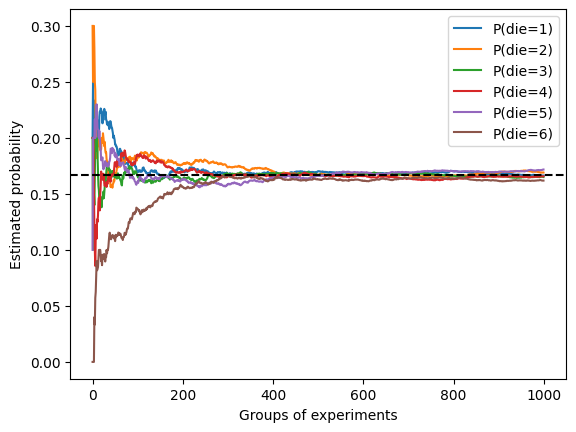
练习 1
# 练习 1 m = 1000, n = 10
counts = tfp.distributions.Multinomial(10, fair_probs).sample(1000)
cum_counts = tf.cumsum(counts, axis=0)
estimates = cum_counts / tf.reduce_sum(cum_counts, axis=1, keepdims=True)
for i in range(6):
plt.plot(estimates[:, i].numpy(),
label=("P(die=" + str(i + 1) + ")"))
plt.axhline(y=0.167, color='black', linestyle='dashed')
plt.gca().set_xlabel('Groups of experiments')
plt.gca().set_ylabel('Estimated probability')
plt.legend();
m = 1000, n = 10
m = 250, n = 40
m = 500, n = 20
练习 3
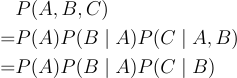
练习 4
如果连续运行同一个测试两次,这两次测试的结果可能会受到相同的系统误差影响。例如,测试设备可能存在某种潜在的偏差,或者测试环境中的某些因素对测试结果产生一致的影响。这样一来,两次测试结果之间的相关性会很高,无法提供额外的独立信息来提高诊断的准确性。
而使用不同特性的两个测试,可以在一定程度上避免这种相关性。第二个测试具有不同的误差模式和检测机制,能够提供与第一个测试相互独立的信息,从而更全面地评估患者的状况。