Is there any trick when applying dropout for improving (test) accuracy? – In this example, by using the dropout approach, the test accuracy on the Fashion-MNIST dataset does not get improved compared to the MLP approach in section 4.3
Specifically, denote gap = accuracy_train (A1) - accuracy_test (A2). By using dropout, I would expect a smaller gap and a smaller A1 due to the regularization property of the dropout. Hence there should not always be guaranteed that the test accuracy A2 will increase.
Hey @Angryrou, yes you supposition is right! We cannot promise there is always an increase of test accuracy. However, what dropout ultimately does is to overcome “Overfitting” and stabilize the training. Once your model is overfitting (like the mlp example), dropout can help.
In practice, we usually use a dropouts of 0.2 - 0.5 ( 0.2 recommended for input layer). Too low dropout cannot have regularization effect, while a too high dropout may lead to underfitting.
Thanks for the reply!
Could you explain more on how the dropout stabilize the training? I do find it more stable in terms of the variance of the activations in each hidden layer (from the exercise 3), but cannot figure out the reason behind. Any intuitive explanation or references should be very helpful!
Hi @Angryrou, here are some intuitions. We pick random neurons to dropout at each epoch, so the layer won’t really too much on one or two specific neuron (i.e., all other neurons have a closed to zero weights)
Suppose we have 4 neurons at one layer, A, B, C, D. With some random unexpected initialization, it is possible that the weights of A & B are closed to zero. Imagine the following two situations:
-
If we don’t have dropout, this layer only relay on neurons C & D to transform information to the next layer. So the neurons A & B might be too “lazy” to adjust its weight since there are C & D.
-
If we set dropout = 0.5, then at each epoch, two neurons are dropped randomly. So it is possible that both C and D are dropped, so A & B have to transform information and adopt the gradients weights adjustment.
Thanks again for the reply. However, I still have some follow up issues unclear:
-
Without the dropout in your example, only 2 of the 4 neurons take effects mostly. In other words, the model may have less representation property (due to smaller capacity in the model) without using dropout. So my understanding from your example is: a model with more capacity should be more stable than a model with less capacity. Is my statement correct?
-
I do not think A & B will be too “lazy” to adjust weights. Assume the model is
y = f(X) = A * x_1 + B * x_2 + C * x_3 + D * x_4, the gradient on A isdl/dy * dy/dAand thedy/dA = x_1, so the adjustment on A is mainly rely on the feature x_1 instead of the value of A.
Hi @Angryrou,
Without the dropout in your example, only 2 of the 4 neurons take effects mostly. In other words, the model may have less representation property (due to smaller capacity in the model) without using dropout. So my understanding from your example is: a model with more capacity should be more stable than a model with less capacity. Is my statement correct?
We don’t dropout during inference, so we still have 4 neurons to keep the original capacity.
I do not think A & B will be too “lazy” to adjust weights. Assume the model is
y = f(X) = A * x_1 + B * x_2 + C * x_3 + D * x_4, the gradient on A isdl/dy * dy/dAand thedy/dA = x_1, so the adjustment on A is mainly rely on the feature x_1 instead of the value of A.
Your intuition is right! Theoretically it depends on the input features and the activation function. So the dropout method “force” the neurons A&B to learn if their features are not as effective as the other neurons’ features.
Thank you. You mentioned
what dropout ultimately does is to overcome “Overfitting” and stabilize the training.
Do you have any recommended papers or blogs that have theoretical support about how dropout can help stabilize the training (e.g., avoid gradient explode and varnish)? I find this is very interesting to explore.
Cheers
Thank you 
I noticed there isn’t test loss. Why?
I have read as following.
https://kharshit.github.io/blog/2018/12/07/loss-vs-accuracy
I noticed that nn.Flatten() haven’t mentioned.
https://pytorch.org/docs/master/generated/torch.nn.Flatten.html
Why do we need to nn.Flatten() first?
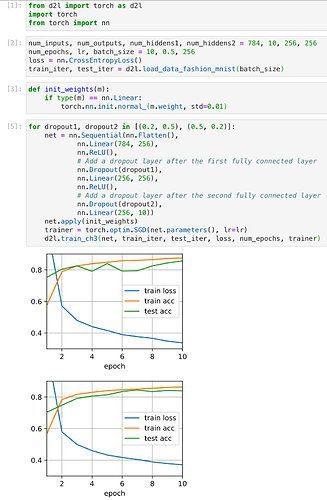
Two pics in 4.6.4.3. Training and Testing and 4.6.5. Concise Implementation are so different?
4.6.7. Exercises
- I have tried to switch the dropout probabilities for layers 1 and 2 by switching dropout1 and dropout2.
Sequential(
(0): Flatten()
(1): Linear(in_features=784, out_features=256, bias=True)
(2): ReLU()
(3): Dropout(p=0.5, inplace=False)
(4): Linear(in_features=256, out_features=256, bias=True)
(5): ReLU()
(6): Dropout(p=0.2, inplace=False)
(7): Linear(in_features=256, out_features=10, bias=True)
)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
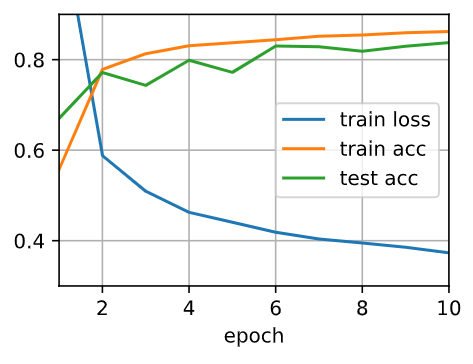
But how can I confirm that the change’s cause is my action of switching the dropout probabilities other than random init?
num_epochs = 20
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
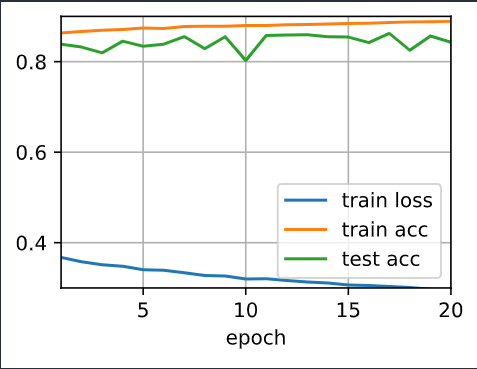
d2l.train_ch3? Does it train continously? I guess so.
You need to reset params before you start training again.
Otherwise you are just updating already trained params.
Also nn.Flatten() is needed to flatten the image into a single vector (28*28=784) for the input of the linear layer.
Cam you check again 4.6.5 and 4.6.4.3 look similar here.
we use .reset_parameters()?
And I found that searching in pytorch docs is so slow. Do you have some good advices?
How similar can we say that these pics are similar?
We can’t expect exactly the same outputs when we have the same inputs?
Hi @StevenJokes, for your question:
I noticed there isn’t test loss. Why?
For any ML problem, we ultimately care about the model performance through evaluation metrics (such as accuracy). However, lots of metrics are not differentiable, hence we use the loss functions to approximate them.
We use loss function just for training’s Backpropagation, and we don’t need to train anymore when we are in test. Similiarly, we just care the final scores of exam instead of the concrete answers.
Do I understand it rightly?
I tried swapping the dropout probabilities for Layers 1 and 2, and did not notice much of a change:
Is there an error in my implementation? Or is this because of the simple nature of the dataset (eg I note that dropout doesn’t help too much over the standard implementation in the first place) and would I normally notice some difference? Thanks!
Hi @Nish, great question! It may be hard to observe a huge loss/acc difference if the network is shallow and can converge quickly. As you can find in the original dropout paper (http://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf) as well, the improvement with dropout on MNIST is less than 1%.