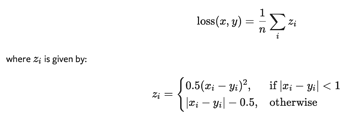Here are my opinions for exs:
If you got any better idea please tell me ,thanks a lot.
Note that I still can’t work out ex.3, and not so sure about ex.5.
ex.1
To get the aggregate loss, I multiply the number of minibatch(X.shape[0]):
@d2l.add_to_class(LinearRegression) #@save
def forward(self, X):
"""The linear regression model."""
#return self.net(X)
return self.net(X)*X.shape[0]
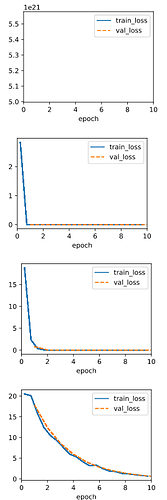
When using the old lr=0.03, the ouput is:
That means the lr is too large, so I divide the lr by the number of minibatch, and the ouput becomes normal.
#model = LinearRegression(lr=0.03)
model = LinearRegression(lr=0.03/1000.)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)

But after read @hy38’s reply I think It’s better to set the paramter reduction=‘sum’ to do that. 
ex.2
?nn.MSELoss
??nn.modules.loss
By search the nn.MSELoss, I find it’s definition path is “…/torch/nn/modules/loss.py”, so I scan this path, and search with keyword ‘Huber’ and find ‘class HuberLoss(_Loss)’, then I test with this code, seems like the Huber’s robust loss regress slower(10 epochs rather than 3 epochs) than the MSELoss and the two errors is close.
@d2l.add_to_class(LinearRegression) #@save
def loss(self, y_hat, y):
fn = nn.HuberLoss()
return fn(y_hat, y)
model = LinearRegression(lr=0.03)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)
print(f'error in estimating w: {data.w - w.reshape(data.w.shape)}')
print(f'error in estimating b: {data.b - b}')
error in estimating w: tensor([ 0.0125, -0.0156])
error in estimating b: tensor([0.0138])
ex.3
After scanning the doc of torch.optim.SGD, I find that the grad is not a self. like parameters, and I can’t find a function to fetch the gard. 
ex.4
I test with this code snippet:
lrs = [3,0.3,0.03,0.003]
for lr in lrs:
model = LinearRegression(lr)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)
Seems like lr=3 is too large that it may produce a lot NaN when computing loss, 0.003 is too small, 0.3 is better than the original 0.03.
ex.5
A. I use this code snippet:
def ex5_20220905(data_sizes, model, trainer):
w_errs = list()
b_errs = list()
for data_size in data_sizes:
data_size = int(data_size)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2,
num_train=data_size, num_val=data_size)
trainer.fit(model, data)
w, b = model.get_w_b()
w_errs.append(data.w - w.reshape(data.w.shape))
b_errs.append(data.b - b)
return w_errs, b_errs
data_sizes = torch.arange(2,2+5,1)
data_sizes = torch.log(data_sizes)*1000
model = LinearRegression(lr=0.03)
trainer = d2l.Trainer(max_epochs=3)
w_errs, b_errs = ex5_20220905(data_sizes=data_sizes, model= model, trainer=trainer)
print(f'data size\tw error\t\t\tb error')
for i in range(len(data_sizes)):
print(f'{int(data_sizes[i])}\t{w_errs[i]}\t\t\t{b_errs[i]}')
| data size |
w error |
|
|
b error |
| 693 |
tensor([ 0.0563, -0.0701]) |
|
|
tensor([0.0702]) |
| 1098 |
tensor([ 0.0002, -0.0004]) |
|
|
tensor([7.6771e-05]) |
| 1386 |
tensor([-0.0010, 0.0001]) |
|
|
tensor([-0.0005]) |
| 1609 |
tensor([ 0.0006, -0.0001]) |
|
|
tensor([0.0003]) |
| 1791 |
tensor([ 1.8096e-04, -4.1723e-05]) |
|
|
tensor([-4.0531e-05]) |
B. Judging from the data above, I think the logarithm growing for data size is more economic way to find a appropriate size of data, because as the data size grows, the same number of data added to the dataset receive less and less effect to reduce the error.(??I’m not so sure about that.)
1 reply