Thanks for reply @goldpiggy !
I also have doubt regarding the normalization of the values. Here the target variable SalePrice is also normalized, which makes its values range from about (-5,5). While submitting predictions to Kaggle what step is taken to get back the range of desired SalePrice values [like 10,000, 20,000]?
1 replySalePrice is the label, and we are not normalizing the label values.
There is a bug in the train_and_pred() function. test_data[‘SalePrice’] = pd.Series(preds.reshape(1, -1)[0]) only return the first prediction. To correct the error, we need to first flatten the ‘preds’ by adding .flatten() after the numpy() and delete the ‘.reshape(1, -1)[0]’
1 replyHi @MorrisXu-Driving, thanks for your suggestion!
I agree that flatten() is a more elegant way, while it seems like these methods have equivalent results. Any other bug exists here?
Hi @Dchaoqun, great question! The normalization step here is to have all the features in the same scales, rather than one feature in range [0,0.1], another in [-1000, 1000]. The later case may lead to some sensitive weights parameters. But you are right, in the real life scenario, we may not know the test data at all, so we will assume the test and train set are following the similar feature distributions.
1 replyHi @goldpiggy, thank you for the clarification!
Hi @goldpiggy,
In the train function, why is MSEloss used as the loss function instead of log_rmse?
I guess,maybe the gradient will be too small due to the derivation of (log(y)-log(y hat))^2.I don’t know if I am right.
A minor point, but in the PyTorch definition of log_rmse :
def log_rmse(net, features, labels):
# To further stabilize the value when the logarithm is taken, set the
# value less than 1 as 1
clipped_preds = torch.clamp(net(features), 1, float('inf'))
rmse = torch.sqrt(torch.mean(loss(torch.log(clipped_preds),
torch.log(labels))))
return rmse.item()
Isn’t the torch.mean() call unnecessary, since loss is already the Mean Squared Error, ie the mean is already taken?
I tried to predict the logs of the prices instead, using the following loss function:
def log_train(preds, labels):
clipped_preds = torch.clamp(preds, 1, float('inf'))
rmse = torch.mean((torch.log(clipped_preds) - torch.log(labels)) ** 2)
return rmse
And the results were much worse. During the k-fold validation step, some of the folds had much higher validation/training losses than the others:
And sometimes the plot of losses didn’t appear to descend with epochs at all:
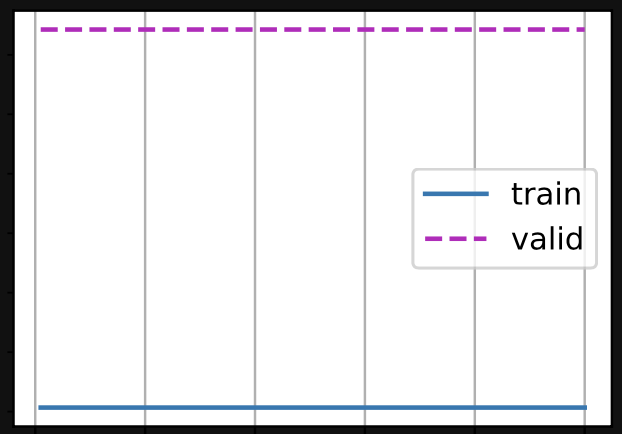
I suppose this is the point of the exercise, to show that it’s a bad idea, but I’m having trouble understanding why. It seems that instead of trying to minimise some concept of absolute error we’re trying to minimise a concept of relative (percentage) error between the prediction and the reality. Why would this lead to such instability?
Edit: I have an idea. In order to maintain numerical stability we have to clamp the predictions:
clipped_preds = torch.clamp(preds, 1, float('inf'))
But if the network parameters are initialised so that all of the initial predictions are below 1 (as is what I observed debugging one run) then they could all get clamped in this way and backprop would fail as the gradients are zero/meaningless?
1 replyHey @Nish, great question! Actually using log_rmse may not be a bad idea. I guess you only change the loss function but not other hyperparameters such as “lr” and “epoch”. Try a smaller “lr” such as 1, and a larger “epoch” such as 1000. What is more, the folds with high loss as 12 here might result from bad initialization, you can try net.initialize(init=init.Xavier() and more details here.)
Thank you @goldpiggy ! So it sounds like my final point could be correct - that the issues came from bad initialisation so that all the initial predictions get clamped to 1 and the gradient is meaningless?
1 replyHey @Nish, you got the idea! Initialization and learning rate are crucial to neural network. If you read further into advanced HPO in later chapters, you will find learning rate scheduler. Keep up!
1 replyHi, @goldpiggy
Analogy:
Hi @swg104, great catch. Would like to post a PR and be a contributor?
(However, since the final loss is divided by “n” double times, it won’t affect the weights optimization.)
@HtC
You will find the orders have same effect.
The reason why we replace missing values with the corresponding features’s mean is to keep the whole’s mean and variance same with the mean and variance before.

I just realized it isn’t same.
Replacing missing values will make variance smaller than before, because the denominator is bigger.
So replacing missing values before standarizing the data will be bigger.
Yes, I was just looking at the same thing.
Hence, what is the correct order?
if you try to predict the logarithm of the price rather than the price?
situation where the values are not missing at random?
done in this section?
Only changing the hyperparameters batch_size=64 and lr=10 can achieve a result of 0.14826.
When the layer is added, although the training loss will be reduced, it will always cause over-fitting. No matter whether you use Dropout or weight attenuation, it is unavoidable.I think this data set is too simple and not suitable for deep networks.

I don’t know if anyone has used the deep network to achieve better results, please share! 
Hi I wonder do we need to initialize the weight and bias before train the model? like using net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
Is the section on Kaggle prediction house price data preprocessing wrong? In the article it says “we apply a heuristic, replacing all missing values by the corresponding feature’s mean.” but in the code it says “Replace NAN numerical features by 0”. Is it better to choose the mean substitution method?
According the formula below:
$E[(x-\mu)^2] = (\sigma^2 + \mu^2) - 2\mu^2+\mu^2 = \sigma^2$
When I use code to test it, the result is not equal, so I am very confused.
a=torch.tensor([1.,2.,3.])
a_mean=a.mean()
print(a_mean) # tensor(2.)
a_var=a.var() # formula: Var(x)=Sum( (x-E(x))**2 )/(n-1)
print(a_var) # tensor(1.)
a_std=a.std()
print(a_std) # tensor(1.)
b=(a-a_mean)**2
print(b)
print(b.mean()) # tensor(0.6667)
print(b.mean()==a_std**2) # tensor(False) ??? why the result not equal
I’m getting the following error when I simply run the code as-is from the tutorial. Can anyone help me understand?
3 repliesHey, bro. I came this error the same.Do you know how to resolve it right now?
In the data preprocessing section, it seems that the code in the book simply standardized the numerical features with mu and sigma computed on a concatenated dataset. Wouldn’t this cause information leak?
Because get_dummies generate bool values. Try this after get_dummies:
features = pd.get_dummies(features, dummy_na=True)
features *= 1
My solutions to the exs: 5.7
In the code below, I wonder how I get the hash value?
class KaggleHouse(d2l.DataModule):
def init(self, batch_size, train=None, val=None):
super().init()
self.save_hyperparameters()
if self.train is None:
self.raw_train = pd.read_csv(d2l.download(
d2l.DATA_URL + ‘kaggle_house_pred_train.csv’, self.root,
sha1_hash=‘585e9cc93e70b39160e7921475f9bcd7d31219ce’))
self.raw_val = pd.read_csv(d2l.download(
d2l.DATA_URL + ‘kaggle_house_pred_test.csv’, self.root,
sha1_hash=‘fa19780a7b011d9b009e8bff8e99922a8ee2eb90’))
The methods from np.ndarray to torch.tensor may be changed, so I use another method to convert np.ndarray to torch.tensor.
train_features = torch.from_numpy(all_features[:n_train].values.astype(float))
test_features = torch.from_numpy(all_features[n_train:].values.astype(float))
train_labels = torch.from_numpy(self.train_data.SalePrice.values.reshape(-1, 1)).to(dtype=torch.float32)
my exercise: