请问下beam search 是如何训练的,作为整个模型的一部分。还是先训练lstm,再训练beam search?
我认为这里不能使用维比特算法来优化是因为预测的概率受序列的影响而不仅仅由输入决定。
假设当前概率只受输入影响,即只受前一阶段输出影响,则:
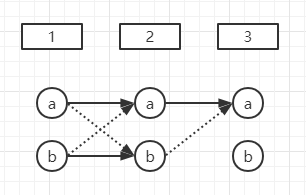
对下图,第3阶段预测为a的概率为第2阶段a和b的最大值,第2阶段a又来自第1阶段a和b的最大值,此时第3阶段预测为a的路径就可以用维比特算法求出来。假设实线比虚线更大,则路径为(a, a, a),但实际上(b, a, a)的概率不一定比(a, a, a)小,只是(b, a, .) < (a, a, .)而已。
概率受整个序列的影响而不仅仅是前一个字符。
这个数值是否是负值, 概率恒小于1大于0, 取log以后是负数。
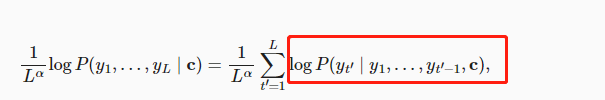
是的, 在视频里面有说明:
我觉得束搜索和Viterbi其实都是可以的。
这里没有采用Viterbi的原因主要是每一步可能的选项太多了,使用Viterbi的开销依然很大。
- Viterbi:O(T*|Y|^2), 这里T是时间步的长度, |Y| 是vocab_size, |Y| 是很大的
- BS: O(T*|Y|*K), 这里K << |Y|, K是人为选定的 束宽(beam size).
在我的理解里面, Beam Search只是一种选择序列的方法, 并没有需要学习的参数叭?
但是你使用束搜索一样会有这种情况呀,可能还是维比特算法计算量比较大
确实,束搜索也没有解决问题,相比维特比算法,计算量小,效率高。
beam search是在预测的时候使用,而且不需要进行训练;训练的时候有真实的标签并且可以计算损失函数。
谢谢大家的回复,如果我们beam search 的score 函数不是训练来的,如何计算每条路径呢的转移概率呢
可以通过将序列的softmax输出相乘得到转移概率
some questions:
q1: 作者在介绍greedy search时的反例与 beam search的实现策略并非一致,后者只是从root节点分支,分支后各自独立。所以说beam search并不能解决反例
q2: greedy search的反例是多数情况吗?毕竟训练时也是按照概率大的来选择的,而且RNN本身有state context机制,难道‘名师出高徒’可能性不大于‘庸师出高徒’?
明显是漏了exp,与bleu类似的。。。
束搜索那里,为什么说是惩罚长序列?log后面那一坨恒为负数,L越大,整个值不是越大(负得越小)吗?而且根据BLEU的原理来看,类似的话也该是惩罚短序列。
把P放到指数上面能说得通,结合上面提到的b站视频这里应该是漏掉了。
尽管求和 $\sum \log P$ 是负值,最大化这个表达式意味着找到概率 (P\left(\mathbf{y}_{t^\prime} \mid \mathbf{y}1, \cdots, \mathbf{y}{t^\prime-1}, \mathbf{c}\right)) 的乘积最大的序列 (\mathbf{y}),即,找到联合概率最大的序列,经过长度归一化后的得分最高的情况。
我觉得还有一个更重要的原因是:常规的自然语言模型不满足马尔可夫性,所以不满足维比特算法适用的前提。
RNN 实现单步计算满足马尔可夫性,但整体序列建模能力超越马尔可夫性,毕竟,通过隐状态传递了历史信息。
