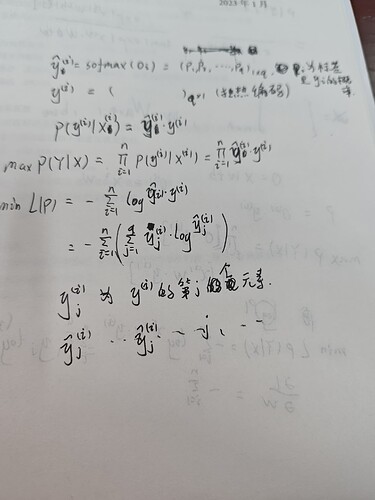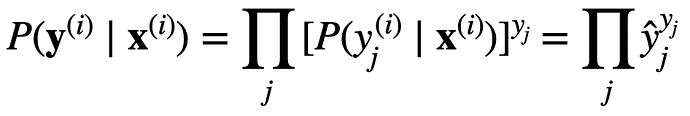滥用n,看得一头雾水,滥用n,看得一头雾水
的确,第一版读的顺畅,内容过度也更自然。
关于3.4.7,在3.4.6中,因为概率向量是一个(0,1,0)的向量,因此发生y_j的概率P就是标签乘以预测值即y_i×y_hat,比如类别2,预测(0.1,0.2,0.7),那么准确预测的概率就是1×0.2,带入3.4.7的中间部分就可以得到信息熵公式
感觉这一小节的顺序有点凌乱,从3.4.7到3.4.8那一步转变很生涩。
通读下来,其实应当是先要介绍信息熵的概念,然后再来介绍 softmax 的损失函数,这样的顺序会更加让人读懂一些。当然,如果能顺带着讲一下 KL散度 的定义(其实信息熵那一小节已经简单介绍了这个概念),让后讲一下 softmax 和 logistic 损失函数的关系就更好了。
1.两边取对数,把“积乘”变成积分, abc取对数后变成 log (a+b+c)
2.最大似然估计,需要让值尽可能大,确定最优的x,两边都*-1后,变成需要让值尽可能的小,确定最优的x
one-hot 向量 所有概率总和为1, 不是0就是1,把通过softmax函数后预测值\hat_y为底数,指数为0的项 \hat_y^0 = 1 指数为1的项 \hat_y^1= \hat_y 所有指数项相乘 ,所有项相乘结果为y, 这是预测y概率分布向量, 取对数后, Log \hat_y ^ y 把真数提取出来
y Log \hat_y, (就如同 log 100 = 2 * log 10 = 2*1 = 2)
读完之后,再来看评论,发现有相似感受的读者。的确,这版的表达别扭!
就是求完导数之后去凑softmax(oj)就行,就是注意那个求和里只需要对exp(oj)那一个量进行求导,不要漏了
请问这里(也就是3.4.7式的第二个等于号)确实是定义的意思吗,书上定义的等号有些地方不写def真的让人难懂
真是的结果 和 模型生成的结果,是相似的,但是不完全一样,那么损失函数就会有梯度,就是有差异,才会有梯度,要不然梯度就是0了
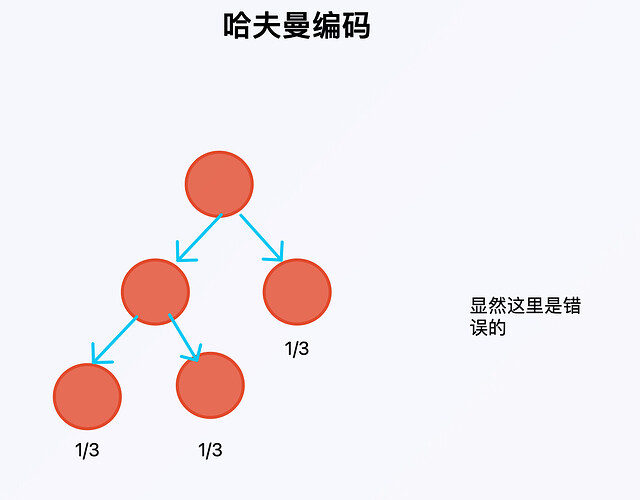
补充一下,哈夫曼编码可以简单理解为一颗二叉树,从树根开始,向左走记0,向右走记1,走到叶子的时候记录叶子结点的编码。
下面这个树中,从左到右的编码依次为00,01,1.
但这里是错的,为什么?
需要来考虑一下哈夫曼树的构造过程,每次选择两个概率最小的节点,然后建立它们的父节点,将父节点替换到原先的节点集合中,重复以上过程直到集合中只有一个节点(即根节点)。
所以,就回答了同样都为1/3的三个节点,没法使用哈夫曼编码来构造。
关于解释softmax中交叉熵损失函数的由来,
预测概率之所以可以被看成当前值在已知数据下的概率,应该是与极大似然的思想有关
同感,第二版读起来很别扭,甚至有些分散我的注意力 ![]()
这书看了一会,有点看不下去了,全是公式和推导,很容易陷入到复杂的细节中。真正的关注点应该是思想,比如softmax的核心是分类,有哪些优势等
我觉得不用改,惊讶的比喻非常妙,恰恰反映出了作者的独特见解。“信息量”这个翻译专业却又古板,跟我们我们本科信息论的说法一致,学的时候就味同嚼蜡,不如惊讶好理解。