thank you, good explanation
I just wondering that in the description is not mentioned that skip connections diminish the vanishing gradient problem (similar like highway networks from Schmidthuber). Or have I overlooked something? Nevertheless: Great Book.
@chris_elgoog I believe you bring up a fair point here.
Although vanishing-gradients aren’t the primary concern of the authors it is indeed mentioned (along with the highway networks you mention) in the Shortcut Connections section of their paper. I’m guessing here, but perhaps they felt like relu activations sufficiently dealt with vanishing-gradient so was no longer a primary concern by that point? 
For the curious, the primary concern the authors are addressing is the degradation problem:
“When deeper networks are able to start converging, a degradation problem has been exposed: with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error […]”
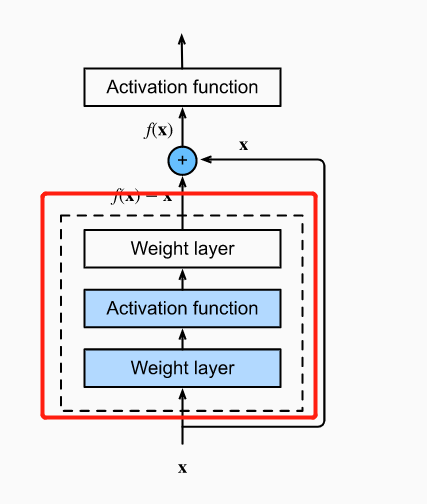
How can I understand that “If the identity mapping f(x)=x is the desired underlying mapping, the residual mapping is easier to learn: we only need to push the weights and biases of the upper weight layer within the dotted-line box to zero”?
i think we can think the process as:
if we add the model of the red box into our bigmodel, but we find the loss is larger than before, what happen in the backward, the backward will make the parameter of the redbox smaller than before, do you remember dropout, if we want to drop some nerual, we will make the output of the nerual to zero, we also can make the parameter (w,b) of the model to zero, so the output will be zero too, so the model of redbox is useless.
so we can pruning the nerual, and we can pruning the part of the model too.
The ResNet paper you reference (He et al, 2016a) uses softmax after the penultimate linear layer, and they use Kaiming He weight initialization. I got the impression that you were replicating the architecture described in the paper, but it seems your code does not softmax the final output and that the weight initialization is Xavier.
Great catch! Yes we did make a simple modification for the best practice. Most of researchers now prefer to use Xavier for initialization since it is more stable.
Residual Block mentioned in Fig: 7.6.2 shows that the network learns F(x) - x, from the original paper it shows it otherwise. Am I missing something ?
Exercises
-
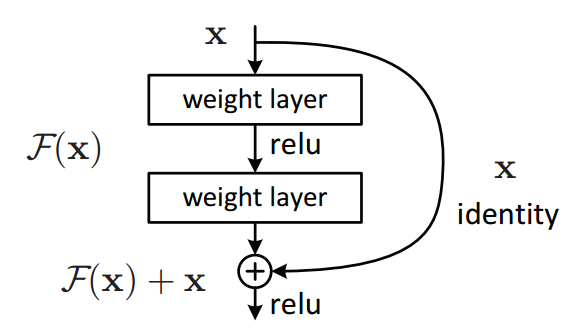
What are the major differences between the Inception block in Fig. 7.4.1 and the residual
block? After removing some paths in the Inception block, how are they related to each other?- Inception uses multiple paths while resnet uses one single path with X.
-
Refer to Table 1 in the ResNet paper (He et al., 2016a) to implement different variants.
-okay. Tried training resnet 34
-
For deeper networks, ResNet introduces a “bottleneck” architecture to reduce model complexity. Try to implement it.
Bottleneck
To increase the network depth whilekeeping the parameter size as low as possible authors introduced bottlenecks
“The three layers are 1x1, 3x3, and 1x1 convolutions, where the 1×1 layers are responsible for reducing and then increasing (restoring) dimensions, leaving the 3×3 layer a bottleneck with smaller input/output dimensions.”class ResidualBottleNeck(ResnetBasicBlock): expansion=4 def __init__(self, in_channels, out_channels, *args, **kwargs): super().__init__(in_channels, out_channels,expansion=4,*args, **kwargs) self.blocks = nn.Sequential( conv_bn(self.in_channels, self.out_channels,self.conv, kernel_size=1), activation_function(self.activation), conv_bn(self.out_channels, self.out_channels,self.conv, kernel_size=3, stride=self.downsampling), activation_function(self.activation), conv_bn(self.out_channels,self.expanded_channels, self.conv, kernel_size=1), activation_function(self.activation) ) -
In subsequent versions of ResNet, the authors changed the “convolution, batch normalization, and activation” structure to the “batch normalization, activation, and convolution”
structure. Make this improvement yourself. See Figure 1 in (He et al., 2016b) for details.- fish classification notebook for details. https://www.kaggle.com/fanbyprinciple/fish-classification-with-resnet/edit/run/75844548
-
Why canʼt we just increase the complexity of functions without bound, even if the function
classes are nested
- vanishing gradients? training timeincrease does not match the accuracy tradeoff.
This is the clearest summary of ResNets I’ve seen anywhere. This book in general is awesome. Thanks so much for making this freely available. Kudos.
Although there is seem be better accuracy on experiment, i don’t understand why it get that. by asssuming “For deep neural networks, if we can train the newly-added layer into an identity function 𝑓(𝐱)=𝐱 , the new model will be as effective as the original model” but how to make sure the some first layers is good? it seem to be if we had the good network then appling new layers by residual block is gettting better result?
here is my code snippet
SO the question is that I don’t know the difference between bn1 and nn.LazyBatchNorm2d(), perhaps I misunderstood the code
bn1=nn.LazyBatchNorm2d()
In the figure 8.6.3, the 1x1 convolution is applied to the input x. The aim of the residual network was to add the block in such a way that the same input could be produced by it. Now, if the channels of the input are itself changed, how will be able to produce the same input? Shouldn’t the 1x1 be applied to the output of the convolutional block so that it has the same dimensions and channels as the input?
class ResNeXtBlock(nn.Module): #@save
"""The ResNeXt block."""
def __init__(self, num_channels, groups, bot_mul, use_1x1conv=False,
strides=1):
super().__init__()
bot_channels = int(round(num_channels * bot_mul))
self.conv1 = nn.LazyConv2d(bot_channels, kernel_size=1, stride=1)
self.conv2 = nn.LazyConv2d(bot_channels, kernel_size=3,
stride=strides, padding=1,
groups=bot_channels//groups) # <-----
self.conv3 = nn.LazyConv2d(num_channels, kernel_size=1, stride=1)
...
I suppose self.conv2 = nn.LazyConv2d(..., groups=bot_channels//groups) should be self.conv2 = nn.LazyConv2d(..., groups=groups).
You proposed my doubt too. I also think it should be groups=groups
There is a bug in the code of Residual class’ __init__. Consider the following call:
blk = Residual(3, strides = 2)
X = torch.randn(4, 3, 6, 6)
blk(X).shape
This call will fail. This is because there is a mismatch between the shapes of X and Y. This happens because use_1x1conv parameter needs to be True in this case, irrespective of whatever the caller sets it to. The fix to catch both the cases will be:
def __init__(self, num_channels, strides=1, use_1x1conv=False):
super().__init__()
self.conv1 = nn.LazyConv2d(num_channels, kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.LazyConv2d(num_channels, kernel_size=3, padding=1)
self.conv3 = None
self.bn1 = nn.LazyBatchNorm2d()
self.bn2 = nn.LazyBatchNorm2d()
if use_1x1conv or strides > 1:
self.conv3 = nn.LazyConv2d(num_channels, kernel_size=1, stride=strides)