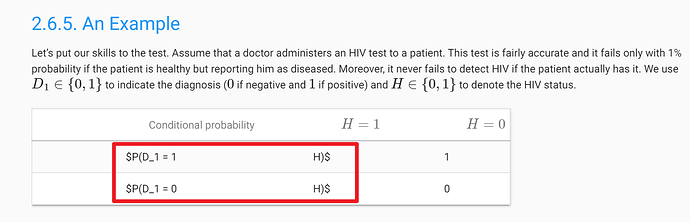
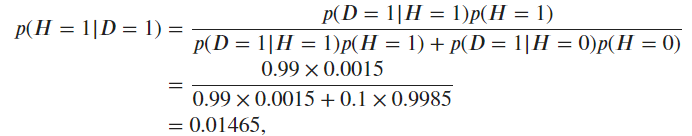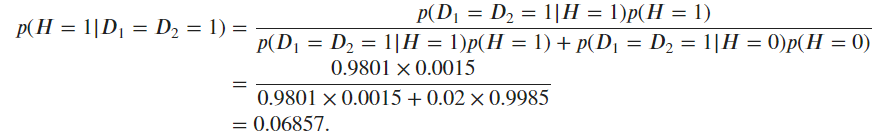There seems to be something wrong with the typesetting.
Yes, the equation is slightly wrong. The updated equation should sum over all possible ‘a’ values in the sample space(a and its complement so that it gets normalized accurately), Reference
An error in exercise 4? It says we draw n samples and then uses m in the definition of zm.
Would have been great and more clear to actually see what numbers you multiplied in the example, for someone never doing stats before, it can be hard to comprehend all the formulas without any explanations.
Answer for Problem 7:
Part 1:
| P(D2=1|H=0) | P(D2=0|H=0) | Total
P(D1=1|H=0) | 0.02 | 0.08 | 0.10
P(D1=0|H=0) | 0.08 | 0.82 | 0.90
Total | 0.10 | 0.90 | 1.00
Part 2:
P(H=1|D1=1) = P(D1=1|H=1) * P(D2=0|H=1) / P(D1=1)
P(D1=1) = P(D1=1,H=0) + P(D1=1, H=1)
=> P(D1=1) = P(D1=1|H=0) * P(H=0) + P(D1=1|H=1) * P(H=1)
Thus, P(H=1|D1=1) = (0.99 * 0.0015) / ((0.10 * 0.9985) + (0.99 * 0.0015)) = 0.01465
Part 3:
P(H=1|D1=1,D2=1) = P(D1=1,D2=1|H=1) * P(H=1) / P(D1=1,D2=1) (1)
P(D1=1,D2=1|H=1) = P(D1=1|H=1) * P(D2=1|H=1) (2)
P(D1=1,D2=1) = P(D1=1,D2=1,H=0) + P(D1=1,D2=1,H=1)
= P(D1=1,D2=1|H=0) * P(H=0) + P(D1=1,D2=1|H=1) * P(H=1) (3)
Using (1), (2), & (3),
P(H=1|D1=1,D2=1) = 0.99 * 0.99 * 0.0015 / (0.02 * 09985 + 0.99 * 0.99 * 0.0015) = 0.06857
Are the above answers correct??
1 Like
“For an empirical review of this fact for large scale language models see Revels et al. (2016).”
I believe this citation is wrong. It links to an auto-grad paper with nothing to do with evaluating LLMs.
I got the same answers independently. Now, we can try and calculate the probability of both of us being wrong.
I have a qustion that, for the first problem of Q7 we have P(D1=1|H=0) = 0.1 but the condition listed above is P(D1=1|H=0) = 0.01 ?
You need to read carefully, it states: P(D1=0|H=1) = 0.01 (false negative). P(D1=1|H=0) = 0.1 (False positive)
Got the same results as well
The same answer. Quite conterintuitive, though. I think it is because the joint FPR 0.02 increased a lot compared to the original example 0.0003. So the positive result can still be confusing to patients.
Ex3.
- The estimated probability
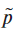is a random variable dependent on 
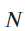that follows the multinomial distribution:
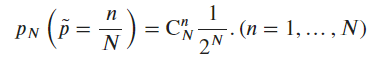
- Expectation
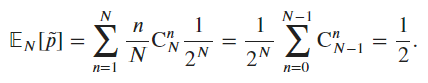
- Variance
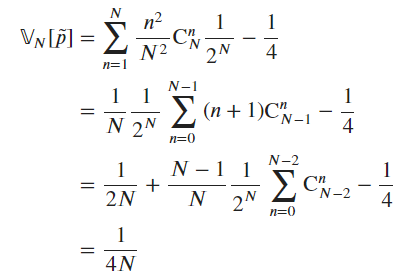
scales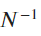
. The convergence rate of 
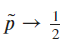is thus 
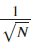, consistent with the CLT.
- Expectation
- According to the Chebyshev Inequality, one has
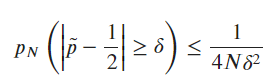
for a given deviation measurement
.
Ex7.
- Note that
and
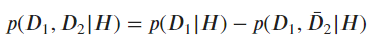
- The conditional probabilities are therefore
- For one test being positive, the positive rate is
which is far from satisfactory since the false positive rate is too high. - For both two tests being positive,
2 Likes
could i ask, for question 3, the variance, how did u get from the 2nd line to the 3rd line? I am a little stuck at that part
Can someone explain the approaches to problems 3, 4, 6 and 8 ??
Hi, I’m confused because it seems you are using “sample size” and “samples” interchangeably.
As a note for the authors, the citation of Revels et. al 2016 in 2.6.7 looks wrong. Maybe this was supposed to be Kaplan et al. 2020, or Hoffmann et al. 2022.
My answers to these exercises:
- Any entirely deterministic process - for example, determining the weight in kilograms of an arbitrary quantity of lithium.
- Any process with stochastic components - for example, predicting tomorrow’s stock prices. One can get to a certain point of accuracy if they closely follow news events and filings, and get good at modeling, but there’s always uncertainty as to the exact decisions others will make. One might argue against such processes existing on fatalist grounds!
- The variance is equal to
p*(1-p) / n. This means the variance scales with1/n, wherenis the number of observations. Using Chebyshev’s inequality, we can bound\hat{p}withP\left(|\hat p - p| \ge k \cdot \sqrt{\frac{p(1-p)}{n}}\right) \le \frac{1}{k^2}(withp=0.5in our case, assuming the coin is fair). Chebyshev’s inequality gives us a distribution-free bound, but asngrows (typically forn > 30), the central limit theorem tells us that\hat p \approx \mathcal{N} \left(p, \frac{p(1-p)}{n}\right) - I’m not sure if I’m interpreting the phrase “compute the averages” correctly, but I wrote the following snippet:
l = 100
np.random.randn(l).cumsum() / np.arange(1, l+1)
As for the second part of the question - Chebyshev’s inequality always holds for a single random variable with a finite variance. You can apply Chebyshev’s inequality to a specific z_m, but you cannot apply it for each z_m independently. This is because the z_ms are not i.i.d. - they share most of the same underlying terms!
5. For P(A \cup B), the lower bound is max(P(A), P(B)), and the upper bound is max(1, P(A) + P(B)). For P(A \cap B), the lower bound is max(0, P(A)+P(B)-1) (remember that P(A)+P(B) can be larger than 1) and the upper bound is min(P(A), P(B))
6. One could factor the joint probability P(A, B, C) as P(C|B) * P(B|A) * P(A), but this isn’t simpler. I’m not sure what exactly this question is looking for.
7. We know that the false positive rate for each test must add up to 0.1, and that the joint probabilities must add up to 1. So the mixed probabilities are 0.08, and P(D_1=0, D_2=0 | H=0) = 0.82. For 7.2, I obtained 1.47%. For 7.3, I obtained 6.86%.
8. The expected return for a given portfolio \boldsymbol \alpha are \boldsymbol \alpha^\top \boldsymbol \mu. To maximize the expected returns of the portfolio, one should find the largest entry in \mu_i and invest the entire portfolio into it - \boldsymbol \alpha should have a single non-zero entry at the corresponding index. The variance of the portfolio is \boldsymbol \alpha^\top \Sigma \boldsymbol \alpha. So the optimization problem described can be formalized as: maximize \boldsymbol \alpha^\top \boldsymbol \mu for some maximum variance \boldsymbol \alpha^\top \Sigma \boldsymbol \alpha, where \sum_{i=1}^n \alpha_i = 1 and \alpha_i \ge 0.