https://d2l.ai/chapter_linear-regression/generalization.html
in the net.initialize(), we did not use parameter initializer package which means we would use the default, it is init.Uniform(scale=0.07), on the other hand we asssume the distribution of data is Gaussian, but why we not use init.Normal() to initialize the parameter? correct me if I am wrong, is there any reason or am I missing something important about the distribution of the data. Thank you.
You are right about it.
And
Check here: 20.1. Generative Adversarial Networks — Dive into Deep Learning 1.0.3 documentation
We can use init.Normal() to initialize the parameter
@goldpiggy
check my answer…
you means that the learned weights should be gauss distribution?
i think the weights should be fit finally to the training set even it’s initiated w/ 0,that’s the meaning of ‘self-learning in ml’.so it’s viable to initiate w/ gauss as well.note the data here should be i.i.d only ,and the noise is assumed to be guass instead.
on the other word,you can use default initialization instead of normal to initiate weiths in mlp sections(i did that too)
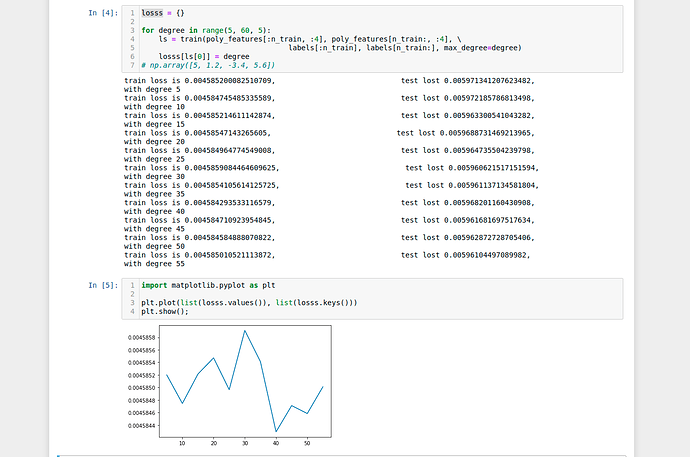
2 Consider model selection for polynomials:
2.1 Plot the training loss vs. model complexity (degree of the polynomial). What do you
observe? What degree of polynomial do you need to reduce the training loss to 0?
Answer - about 40
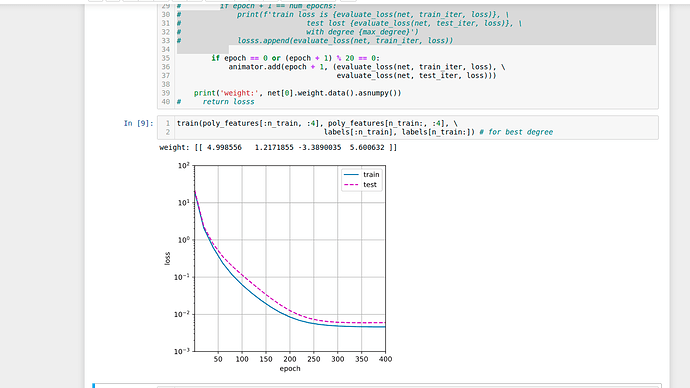
2.2 Plot the test loss in this case
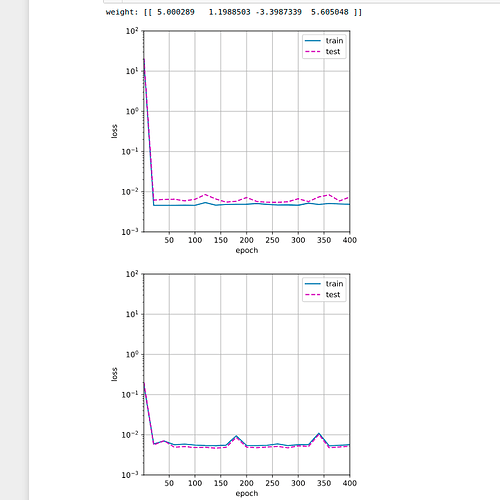
Answer here is plot for polynomial degree 40 (best degree found in 2.1)
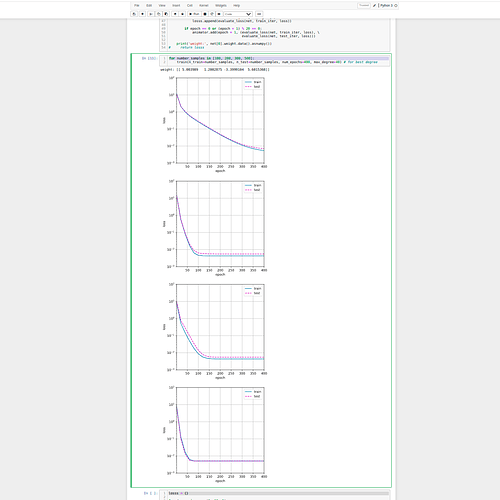
2.3 Generate the same plot as a function of the amount of data.
Answer: with same degree of polynomials (40 from 2.1), number of epoch (400) I find next:
- as number train, test example are growing - algorithm is converging quicker
- after some point of increasing number of examples , train / test loss become very close.
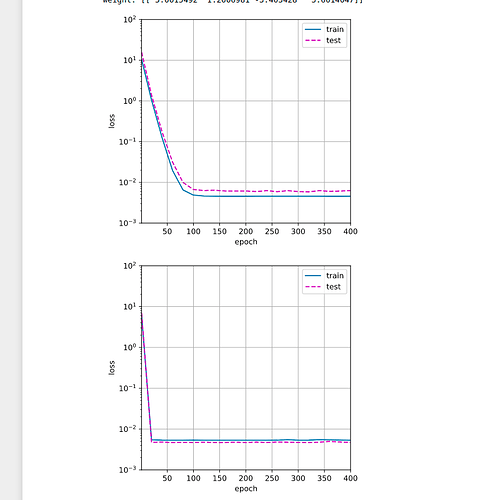
- What happens if you drop the normalization (1/i!) of the polynomial features x i ? Can you
fix this in some other way?
Answer 3.1 If we drop that type of normalization, we have a situation where our loss is not decreasing
Here is graph
3.2 We can use standard approach to scale data z = (x - u) / s, where u is the mean of the training samples and s is the standard deviation of the training samples.
So results is better, here
- Can you ever expect to see zero generalization error?
Answer -> I suppose it is not possible in reality