- why we should not divide it with batch size?
- What does param.data.sub_() function do?
- Where we can learn or find about such functions?
i know its silly…but need help
- Because maybe the number of examples cannot be divided by batch size. For e.g, we have 105 examples and batch size was set to 10. That’s why we use
indices[i:min(i+batch_size, num_examples)]
to catch the last batch whose size is less than 10. - tensor_a.sub_(tensor_b) is equivalent to tensor_a = tensor_a - tensor_b
sub_() is an in-place function.
I suggest you to test the function by some simple data to see the result, or you can just google it.
1 Like
There is no mistake. For the reason why param.grad is divided by batch_size, you can learn the knowledge of the computational graph. You will find the reason in that part.
More epochs to train will also bring you the right answer. 
1 Like
Q2: Assume that you are Ohm trying to come up with a model between voltage and current. Can you use auto differentiation to learn the parameters of your model?
A2: You could set the feature of the model to be either V for voltage or I for current. Then, you could take measurements of V as a function of I or I as a function of V on a given conductor to obtain a set of measured of feature-label pairs. Then, these pairs could be used to fit a linear regression model through the gradient descent technique. The weights obtained in the process would (approximately) correspond to the resistance of the conductor from which the measurements were taken. However, these model would give poor prediction results for different conductors with varying resistance. A linear regression model should be built for different conductors. (Remember Ohm’s law V = R*I)
Q4: What are the problems you might encounter if you wanted to compute the second derivatives? How would you fix them?
A4: Apparently, there is no straightforward manner to compute second order derivatives of our loss function using MxNet. However, any differential equation of order n can be written as a system of n differential equations of first order. By solving all of these ODEs of first ordre one could arrive to the solution, but I’m not sure how to implement it. Any suggestions?
Hi, wonderful tutorial and explanation. I have one question about the final training loop:
What does l.sum().backward() do?
I can’t seem to find any change the value of in L or any of the other tensors before or after this step.
It computes the gradient of the tensor l.sum() with respect to w and b. Here is the documentation for this method.
The change is in the gradients, which are stored at the “free variables” w and b with respect to which the gradients are computed. You can retrieve these gradients, and see that they indeed change before and after a call to backward(), by inspecting the grad attribute of these variables, like so: w.grad , b.grad .
Why do we need param.grad.zero_() in sgd function?
In the function sgd(params, lr, batch_size) this line baffles me:
param -= lr * param.grad / batch_size
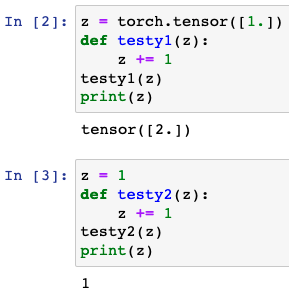
How is it possible for this line to update the external scope variable “w”? I did some testing and found the below behavior. Why does the first example update “z” whereas the second does not. Are scope rules different for PyTorch tensors?
1 Like
My solution about Exercise 2:
in thedata_iter, why batch_indices has to be converted to torch.tensor? a list also works, is there any particular consideration?
In section 3.4.4, we added a fit_epoch function to the Trainer class (copied below).
@d2l.add_to_class(d2l.Trainer) #@save
def fit_epoch(self):
self.model.train()
for batch in self.train_dataloader:
loss = self.model.training_step(self.prepare_batch(batch))
self.optim.zero_grad()
with torch.no_grad(): # why we use torch.no_grad() here??
loss.backward()
if self.gradient_clip_val > 0:
self.clip_gradients(self.gradient_clip_val, self.model)
self.optim.step()
self.train_batch_idx += 1
if self.val_dataloader is None:
return
self.model.eval()
for batch in self.val_dataloader:
with torch.no_grad():
self.model.validation_step(self.prepare_batch(batch))
self.val_batch_idx += 1
Inside the training loop (for batch in self.train_dataloader: …), why we enable the torch.no_grad() context manager?
According to pytorch’s doc: torch.no_grad() is a context-manager that disabled gradient calculation.
Disabling gradient calculation is useful for inference, when you are sure that you will not call Tensor.backward(). It will reduce memory consumption for computations that would otherwise have requires_grad=True.
However, we need to explicitly call loss.backward() within the training loop.
1 Like
My opinions for the exs:
I’ m not so sure about ex.7and ex.9 can anybody help me?
ex.1
1.Initialize the w to zeros.
2. Initialize w by norm distribution.
3. Initialize the w by norm distribution with sigma set to 1000
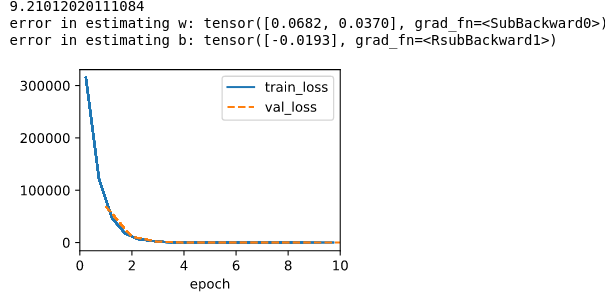
Note that I set max epoch to 10, seems like if I start w with all zero, it doesn’t make any difference, but if I change the sigma from 0.01 to 1000, the training speed doesn’t change, but the training error start with a huge quantity, and ends with a number increase by two orders of magnitude for both w and b.
ex.2
Step1 I produce a class to generate the examples composed by self.V = voltage, self.I = current, self.IR = I*R
%matplotlib inline
import torch
from d2l import torch as d2l
import random
class SyntheticRegressionData_202209031839(d2l.DataModule):
def __init__(self, r_list, noise=0.1, num_train=100, num_val=100, batch_size=32, shuffle=True):
super().__init__()
self.save_hyperparameters()
#for every resistor r, send some voltage and get some current
#assume that the voltage is the range(1,num_train+1,1)
V_train = torch.tensor([])
V_val = torch.tensor([])
I_train = torch.tensor([])
I_val = torch.tensor([])
IR_train = torch.tensor([])# to save the value of I*R
IR_val = torch.tensor([])
for r in r_list:
#V_train_tmp=torch.abs(torch.randn(num_train, 1))
V_train_tmp = torch.tensor(range(1,num_train+1,1)).reshape(-1,1)
V_train = torch.cat((V_train, V_train_tmp), 0)
I_train_tmp = V_train_tmp/r + torch.randn(num_train, 1) * noise
I_train = torch.cat((I_train, I_train_tmp), 0)
IR_train = torch.cat((IR_train, I_train_tmp*r), 0)
for r in r_list:
V_val_tmp = torch.tensor(range(1,num_val+1,1)).reshape(-1,1)
V_val = torch.cat((V_val, V_val_tmp), 0)
I_val_tmp = V_val_tmp/r + torch.randn(num_val, 1) * noise
I_val = torch.cat((I_val, I_val_tmp), 0)
IR_val = torch.cat((IR_val, I_val_tmp*r), 0)
#need to be suffle or the examples will be ordered by the r value
indices_train = list(range(0, self.num_train*len(r_list)))
indices_val = list(range(0, self.num_train*len(r_list)))
if shuffle:
random.shuffle(indices_train)
random.shuffle(indices_val)
#combine examples for training and validating
self.V = torch.cat((V_train[indices_train], V_val[indices_val]), 0)
self.I = torch.cat((I_train[indices_train], I_val[indices_val]), 0)
self.IR = torch.cat((IR_train[indices_train], IR_val[indices_val]), 0)
Step2 As I experimented with 2 different resistors, each one will be put voltage(I) vary from 1 to 100, and I evaluate the current(I), and plot them, judging from the image, the relation between I and V of the same resistor is linear.
import matplotlib.pyplot as plt
data_1= SyntheticRegressionData_202209031839([1])
data_2= SyntheticRegressionData_202209031839([2])
plt.plot(data_1.V, data_1.I, 'o', data_2.V, data_2.I, 'o')
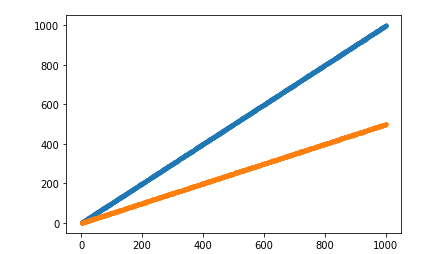
Step3 Define the data loader.
@d2l.add_to_class(SyntheticRegressionData_202209031839)
def get_dataloader(self, train):
#the real num_train is num_train*len(self.r_list)
i = slice(0, self.num_train) if train else slice(self.num_train, None)
return self.get_tensorloader((self.IR, self.V), train, i)
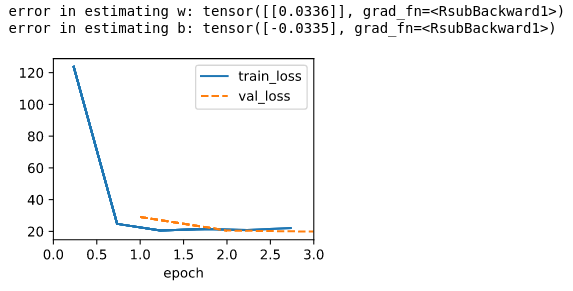
Step4 Train the model, learning rate is suggested to set to a small value, or it will get many NAN at the forward phase, and the conclution is that U = I*R.
data= SyntheticRegressionData_202209031839(r_list = range(1,11,1))
model = LinearRegressionScratch(1, lr=0.0003, sigma = 0.01)
trainer = d2l.Trainer(max_epochs=3)
trainer.fit(model, data)
print(f'error in estimating w: {1. - model.w}')
print(f'error in estimating b: {0. - model.b}')
ex.3
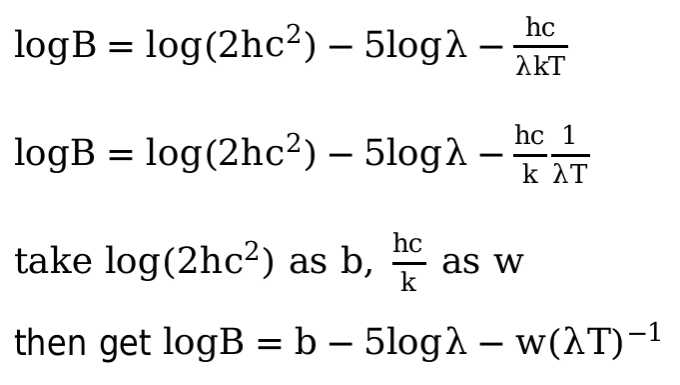
As the procedure shown in the picture, I think during the experiment, the λ, B, T can be preprocessed as logB, -5logλ, (λT)^-1, where logB will be the y, -5logλ and (λT)^-1 will be x1 and x2. Then the problem become a linear regression, after we have train out the w and b, we can use it to compute T with a B and λ.
ex.4
I tested with a simple linear function.
def loss(y_hat, y):
l = (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
return l.mean()
x = torch.tensor([[1.,2.],[3.,4.]])
b = torch.tensor([1.]).requires_grad_(True)
w = torch.tensor([1.,2.]).reshape(-1,1).requires_grad_(True)
y_hat = (torch.matmul(x, w) + b)
y = torch.tensor([5.,6.])
loss = loss(y_hat, y)
loss.backward()
print(w.grad, b.grad)
loss.backward()
print(w.grad, b.grad)
The first backward works well , and the grad is tensor([[ 9.5000], [13.0000]]) tensor([3.5000])
But the second backward one cause a error:
RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
As the ouput say, I should add “retain_graph=True” at the first backward() or the grad will be drop each automatically. So I change the code at the first backward to
loss.backward(retain_graph=True)
and the output is:
tensor([[ 9.5000], [13.0000]]) tensor([3.5000])
tensor([[19.], [26.]]) tensor([7.])
ex.5
I think because the element-wise subtraction can only be used between two tensors with same shape, unless one of them is a scalar.
ex.6
I use the same synthetic data in this chapter, test lr = [0.003, 0.03, 0.3, 3] with max_epoch = 3, and find that 0.03 is too small that the reducing of error(both train and val) is too slow, 3 is too large that the error keep growing as the epoch proceed, 0.3 is the fast one that reach 0 error before the first epoch.
Then I use max_epoch = 10 to see what’s happen, it works well for the lr=0.003, but still not enough, and makes little difference to lr=0.3 and lr=0.03 cause I think they have already reached a tiny error within 3 epochs, and besides, the error of lr=3 still growing.
May be lr =3 is too large compared to the scale of w and b.
ex.7
I added the code below into the function fit_epoch(), and can see some 8 in the output.
if batch[0].shape[0] != 32:
print(batch[0].shape[0])
So maybe the data_iter just give out all the examples out to train or validate when the number can’t match the batch size.
ex.8
A I tested with those two code snippets below, while the data keeps the same, seems like the training drops sharply at the beginning but then floating near a error that is not that ideal, but the validate eroor is always small than the train error.
@d2l.add_to_class(LinearRegressionScratch) #@save
def loss(self, y_hat, y):
l = (y_hat - d2l.reshape(y, y_hat.shape)).abs().sum()
return l.mean()
model = LinearRegressionScratch(2, lr=0.03, sigma = 0.01)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)
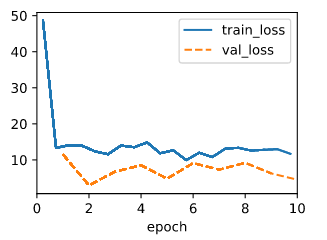
B I use this code to perturb,
data.y[4] = 10000
The output for squared loss is:
The output for abs loss is:
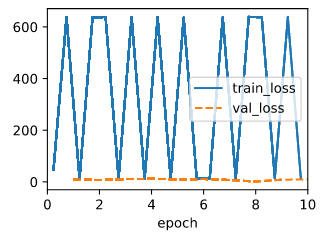
Judging from the result, seems like the squared loss is more vulnerable to large value.
C The abs loss is fast and robust to large value, the squared loss is more accurate.
Maybe I can use the sqrt of the mean squared error.
@d2l.add_to_class(LinearRegressionScratch) #@save
def loss(self, y_hat, y):
l = (y_hat - y.reshape(y_hat.shape)) ** 2
l = l.sum().mean().pow(0.5)
return l
And the test:
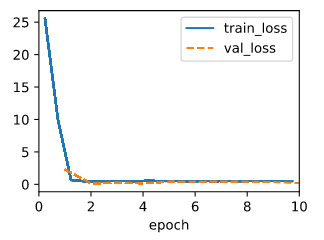
model = LinearRegressionScratch(2, lr=0.03, sigma = 0.01)
trainer = d2l.Trainer(max_epochs=10)
data = d2l.SyntheticRegressionData(w=torch.tensor([2, -3.4]), b=4.2)
trainer.fit(model, data)
ex.9
I think it’s to break the relation between the data because we don’t need that information.
The shuffle fuction in random package is still run under a predictable formula, so the shuffle is also not that reliable(? I’m not so sure about that).
Like the code I used in ex.2 to produce voltage and current, if I don’t use shuffle, the data will be arranged in the order of the resistor, in other words, the voltage and current get from the same resistor is near to each other.
Also confused here, any one has an idea?
IMO the reason is to not track gradients when updating the weights;
With torch.no_grad() block means doing these lines without keeping track of the gradients, in order to not update the gradients when it is updating the weights as that would affect the backdrop.
check this thread
because gradient will be accumulated in grad attribute every batch or mini batch by default. see link
Because tensor type is not immutable, python pass it by reference and can change its value inside function. But int type is immutable, python pass it by value and create a new object(int 2) which is then pointed by z in testy2. the value of z outside testy2 is not influenced.
ex.4 your answer is wrong. You can not just backward twice to get 2-order differential. pytorch will accumulate the grad if you do not use grad.zero_()to zero it. Don’t you find the result of the second backward is just twice that of firse backward? You can reference to the code below
import torch
x = torch.randn((2), requires_grad=True)
y = x**3
dy = torch.autograd.grad(y, x, grad_outputs=torch.ones(x.shape),
retain_graph=True, create_graph=True)
dy2 = torch.autograd.grad(dy, x, grad_outputs=torch.ones(x.shape))