Thanks for your reply. below is all my code.
%matplotlib inline
from d2l import torch as d2l
import torch
import random
def synthetic_data(w, b, num_examples):
""" Generate y = Xw + b + noise. """
X = torch.normal(0, 1, (num_examples, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
print('features:', features[0], '\nlabel:', labels[0])
features: tensor([ 0.5924, -1.3852])
label: tensor([10.1155])
d2l.set_figsize()
# The semicolon is for displaying the plot only
d2l.plt.scatter(d2l.numpy(features[:, 1]), d2l.numpy(labels), 1)
<matplotlib.collections.PathCollection at 0x7f18c1d59750>
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
#The examples are read at random, in no particular order
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(
indices[i:min(i+batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, '\n', y)
break
tensor([[-0.9675, 0.7085],
[ 0.8437, -0.6500],
[ 0.1811, 1.1862],
[-0.3506, 0.0772],
[ 0.3116, 0.9374],
[ 0.5395, 0.6735],
[ 1.2217, -0.2031],
[-1.3825, -1.7679],
[ 1.2293, 0.1035],
[ 1.2081, 0.4335]])
tensor([[-0.1261],
[ 8.0838],
[ 0.5244],
[ 3.2267],
[ 1.6360],
[ 2.9801],
[ 7.3324],
[ 7.4362],
[ 6.3053],
[ 5.1291]])
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
def linreg(X, w, b):
"""The linear regression model."""
return torch.matmul(X, w) + b
def squared_loss(y_hat, y):
"""Squared loss."""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
def sgd(params, lr, batch_size):
"""Minibatch stochastic gradient descent."""
for param in params:
param.data.sub_(lr*param.grad/batch_size)
param.grad.data.zero_()
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # Minibatch loss in 'X' and 'y'
# Compute gradient on 'l' with respect to ['w', 'b']
l.sum.backward()
sgd([w, b], lr, batch_size) # Update parameters using their gradient
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch{epoch+1}, loss{float(train_l.mean()):f}')
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
<ipython-input-23-fa7fa5fdb2c8> in <module>
8 l = loss(net(X, w, b), y) # Minibatch loss in 'X' and 'y'
9 # Compute gradient on 'l' with respect to ['w', 'b']
---> 10 l.sum.backward()
11 sgd([w, b], lr, batch_size) # Update parameters using their gradient
12 with torch.no_grad():
AttributeError: 'builtin_function_or_method' object has no attribute 'backward'
to find whether a function have mentioned before.
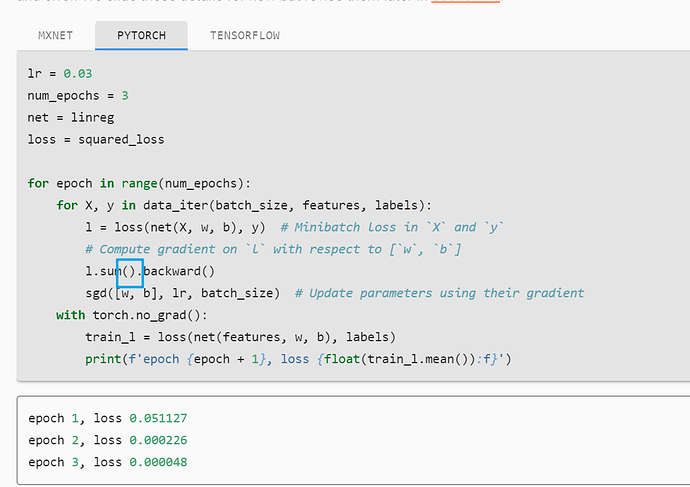
I am too careless
