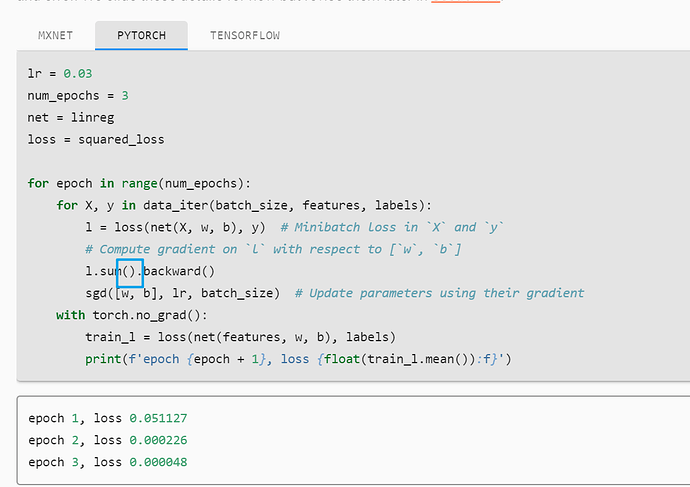
Does it mean that it shouldn’t work when using the correct l.sum?

I think that gradient is 0 when W is ones. Why moving in the right direction?
Hi @StevenJokes, Sorry, in my reply, I was not explaining your question about weight initialization. I probably missed that question. I was explaining the reason it works for l.mean() (Which is obviously wrong and has been fixed now.) given everything remains the same.
So, now, to answer your question about zero weight init, let me explain below.
Here we are using a simple squared error loss function/cost function.
When you use a convex cost function (has only one minima), you can initialize your weights to zeros and still reach the minima. The reason is that you’ll have just a single optimal point and it does not matter where you start by initializing the weights. Though, the starting point may change the epochs it takes to reach optimum you are bound to reach it. On the other hand in neural networks with the hidden layers the cost function doesnt have one single optimum and in that case to break the symmetry we don’t want to use same weights.
If y = b , then gradient is 0.
I think that gradient is 0 when W is zeros. Why moving in the right direction ?
I have understand that convex cost function has only one minima .
But param.data.sub_(lr*param.grad/batch_size) will make sure that param doesn’t change, if grad == 0. 
Then how to get the only minima without params changed  ?
?
I didn’t understand the relation between
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # Minibatch loss in X and y
and
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
Why did we use features to replace x and use labels to replace y?
Can you explain The features and tags of mini-batch examples are given by X
# and y respectively in more detail?
- set y as voltage and set x as current.
- No, I can’t.
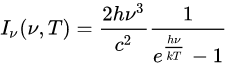
I can’t separate variables v and T in e^(hv/KT).
y.backward(retain_graph=True)
- true_w has one row and len(w) columns, but w has len(w) rows and one column.
- set
lr = your_num - In the last loop of
for i in range(0, num_examples, batch_size)::j = torch.tensor(indices[i: num_examples)
@StevenJokes your understanding of graadients is wrong.
Let me give you a high school example.
Let’s say.
y= wx (Where x is a constant)
The dy/dw = x It doesn’t matter what the value of w is. Gradient is always x.
Get the point?
Similarly when weights are set to zero. gradient is not zero.
If you don’t believe me and you want to print out the gradient value to check:
Then do this small experiment.
X = torch.ones(10,2)
w = torch.zeros((2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
y = torch.matmul(X, w) + b
y.sum().backward()
print(w.grad)
>>>tensor([[10.],
[10.]])
print(X.sum(dim=0))
>>>tensor([10., 10.])
I just knew that gradient is dy/dw instead of dy/dx. 
We calculate the derivates with respect to weights and not the inputs.
Is this clear now?
Thanks a lot. I got it why I was worry.
You meant my github’s issue?
My issue is about " 2.5.2 does’t have PyTorch’s version."
I have heard that Variable has merge into tensor from zhihu.
Is it right?
If so, 2.5.2 doesn’t need PyTorch’s version.
I have replied to the thread. I think that will answer your questions.
Yes, I meant closing the issue on github if your doubt is solved.
Could anyone explain why in the pytorch implementation we have implemented the line param.grad.data.zero_() ?
Why are we setting the gradients of the parameters to 0 after subtracting them from the parameter values? I made my model without this line and my loss kept increasing and reached inf. Also the values of my parameters w, b are large negative values.
# PyTorch accumulates the gradient in default, we need to clear the previous
# values.
x.grad.zero_()
in http://preview.d2l.ai/d2l-en/PR-1080/chapter_preliminaries/autograd.html!
You can use the searching  to find whether a function have mentioned before.
to find whether a function have mentioned before.
When I run the training code, I got the error:
‘AttributeError: ‘builtin_function_or_method’ object has no attribute ‘backward’’
with l.sum.backward()
How could a loss function we defined by ourselves be autograded ?
I can’t give your answer without the whole code you ran. Please publish your all code you ran.
Thanks for your reply. below is all my code.
%matplotlib inline
from d2l import torch as d2l
import torch
import random
def synthetic_data(w, b, num_examples):
""" Generate y = Xw + b + noise. """
X = torch.normal(0, 1, (num_examples, len(w)))
y = torch.matmul(X, w) + b
y += torch.normal(0, 0.01, y.shape)
return X, y.reshape((-1, 1))
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
print('features:', features[0], '\nlabel:', labels[0])
features: tensor([ 0.5924, -1.3852])
label: tensor([10.1155])
d2l.set_figsize()
# The semicolon is for displaying the plot only
d2l.plt.scatter(d2l.numpy(features[:, 1]), d2l.numpy(labels), 1)
<matplotlib.collections.PathCollection at 0x7f18c1d59750>
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
#The examples are read at random, in no particular order
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(
indices[i:min(i+batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, '\n', y)
break
tensor([[-0.9675, 0.7085],
[ 0.8437, -0.6500],
[ 0.1811, 1.1862],
[-0.3506, 0.0772],
[ 0.3116, 0.9374],
[ 0.5395, 0.6735],
[ 1.2217, -0.2031],
[-1.3825, -1.7679],
[ 1.2293, 0.1035],
[ 1.2081, 0.4335]])
tensor([[-0.1261],
[ 8.0838],
[ 0.5244],
[ 3.2267],
[ 1.6360],
[ 2.9801],
[ 7.3324],
[ 7.4362],
[ 6.3053],
[ 5.1291]])
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
def linreg(X, w, b):
"""The linear regression model."""
return torch.matmul(X, w) + b
def squared_loss(y_hat, y):
"""Squared loss."""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
def sgd(params, lr, batch_size):
"""Minibatch stochastic gradient descent."""
for param in params:
param.data.sub_(lr*param.grad/batch_size)
param.grad.data.zero_()
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # Minibatch loss in 'X' and 'y'
# Compute gradient on 'l' with respect to ['w', 'b']
l.sum.backward()
sgd([w, b], lr, batch_size) # Update parameters using their gradient
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch{epoch+1}, loss{float(train_l.mean()):f}')
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
<ipython-input-23-fa7fa5fdb2c8> in <module>
8 l = loss(net(X, w, b), y) # Minibatch loss in 'X' and 'y'
9 # Compute gradient on 'l' with respect to ['w', 'b']
---> 10 l.sum.backward()
11 sgd([w, b], lr, batch_size) # Update parameters using their gradient
12 with torch.no_grad():
AttributeError: 'builtin_function_or_method' object has no attribute 'backward'
You should use l.sum().backward().
Try to contrast with the code given before you ask please, and it is quicker and useful usually.
Thinks! forgive my stupid mistake  I am too careless
I am too careless
This is a minor point, and doesn’t affect the main ideas of this exercise. But I believe that the SGD result should be compared against the analytic least-squares solution, not against the true_w and true_b. The reason is that the best solution from least-squares is also unlikely to match true_* because of sampling variability in the noise. That is to say, the real best solution here is not the initial parameters; it’s the least-square solution to the observed data.
Not a big deal here, because the noise is small relative to the effect size. But I thought I would point it out anyway.
Great book so far! Thanks!