https://d2l.ai/chapter_linear-regression/linear-regression-scratch.html
In the 3.2.7 training part, the pytorch implementation for getting w and b did a much worse job
compared to the 3.3.7, where applied built-in pytorch functions. E.g., the error for predicting b is 1.8039 in 3.2.7 but -0.0006 in 3.3.7.
I tried to dive into but failed to find the reason. Could anyone help? It is not reasonable that the error were not in the same order of magnitude.
P.S. both the mxnet implementations in 3.2.7 and 3.3.7 achieved w and b close to their real value. E.g., the error for predicting b are 0.00049448 and 0.00026846 respectively according to the notebook (also my local test with similar results)
Looks like in sgd function for pytorch, it should not divide param.grad by batch_size, because in main loop, it did l.mean().backward()
Thanks for point out this! I do not think the sgd function has problem – It follows the definition. Rather I feel it would make more sense to change l.mean().backward() to l.sum().backward().
def sgd(params, lr, batch_size): #@save
for param in params:
param.data.sub_(lr*param.grad/batch_size) # this line cause the problem, we don’t divide by batch_size, if you try with param.data.sub_(lr*param.grad) you will get a right result
param.grad.data.zero_()
Just as the same as the above discussion. The “l.mean().backward()” has already calculated the mean of the 10-dimensional loss vector. Now we get back to the sgd(), the “param.data.sub_(lr * param.grad / batch_size)” is undoubtedly wrong as the update is divided by batch_size again. That is why the two different implementation has different performance. Once you correct sgd() by deleting “/batch_size”, you will get the correct answer
w = torch.zeros(size=(2,1), requires_grad=True)
w
tensor([[0.],
[0.]], requires_grad=True)
lr = 0.03 # Learning rate
num_epochs = 3 # Number of iterations
net = linreg # Our fancy linear model
loss = squared_loss # 0.5 (y-y')^2
for epoch in range(num_epochs):
# Assuming the number of examples can be divided by the batch size, all
# the examples in the training data set are used once in one epoch
# iteration. The features and tags of mini-batch examples are given by X
# and y respectively
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # Minibatch loss in X and y
l.mean().backward() # Compute gradient on l with respect to [w,b]
sgd([w, b], lr, batch_size) # Update parameters using their gradient
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch+1}, loss {float(train_l.mean())}')
epoch 1, loss 4.442716598510742
epoch 2, loss 2.3868186473846436
epoch 3, loss 1.2835431098937988
Still works. Why? What difference with the question as follow? I think autograd would fail, but it didn’t.
Now, w isn’t zeros too. Really confused  .
.
w
tensor([[ 1.1457],
[-2.0979]], requires_grad=True)
@GentRich @ouafo_mandela @Angryrou Thanks for catching this bug. We’ll fix this asap.
Also @StevenJokes it still works because by diving an extra time by batch size we have just scaled down the gradients but we are still moving in the right direction towards the local minima. But technically l.sum() is correct not l.mean().
Does it mean that it shouldn’t work when using the correct l.sum?

I think that gradient is 0 when W is ones. Why moving in the right direction?
Hi @StevenJokes, Sorry, in my reply, I was not explaining your question about weight initialization. I probably missed that question. I was explaining the reason it works for l.mean() (Which is obviously wrong and has been fixed now.) given everything remains the same.
So, now, to answer your question about zero weight init, let me explain below.
Here we are using a simple squared error loss function/cost function.
When you use a convex cost function (has only one minima), you can initialize your weights to zeros and still reach the minima. The reason is that you’ll have just a single optimal point and it does not matter where you start by initializing the weights. Though, the starting point may change the epochs it takes to reach optimum you are bound to reach it. On the other hand in neural networks with the hidden layers the cost function doesnt have one single optimum and in that case to break the symmetry we don’t want to use same weights.
If y = b , then gradient is 0.
I think that gradient is 0 when W is zeros. Why moving in the right direction ?
I have understand that convex cost function has only one minima .
But param.data.sub_(lr*param.grad/batch_size) will make sure that param doesn’t change, if grad == 0. 
Then how to get the only minima without params changed  ?
?
I didn’t understand the relation between
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # Minibatch loss in X and y
and
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
Why did we use features to replace x and use labels to replace y?
Can you explain The features and tags of mini-batch examples are given by X
# and y respectively in more detail?
- set y as voltage and set x as current.
- No, I can’t.
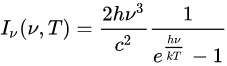
I can’t separate variables v and T in e^(hv/KT).
y.backward(retain_graph=True)
- true_w has one row and len(w) columns, but w has len(w) rows and one column.
- set
lr = your_num - In the last loop of
for i in range(0, num_examples, batch_size)::j = torch.tensor(indices[i: num_examples)
@StevenJokes your understanding of graadients is wrong.
Let me give you a high school example.
Let’s say.
y= wx (Where x is a constant)
The dy/dw = x It doesn’t matter what the value of w is. Gradient is always x.
Get the point?
Similarly when weights are set to zero. gradient is not zero.
If you don’t believe me and you want to print out the gradient value to check:
Then do this small experiment.
X = torch.ones(10,2)
w = torch.zeros((2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
y = torch.matmul(X, w) + b
y.sum().backward()
print(w.grad)
>>>tensor([[10.],
[10.]])
print(X.sum(dim=0))
>>>tensor([10., 10.])
I just knew that gradient is dy/dw instead of dy/dx. 
We calculate the derivates with respect to weights and not the inputs.
Is this clear now?
Thanks a lot. I got it why I was worry.
You meant my github’s issue?
My issue is about " 2.5.2 does’t have PyTorch’s version."
I have heard that Variable has merge into tensor from zhihu.
Is it right?
If so, 2.5.2 doesn’t need PyTorch’s version.
I have replied to the thread. I think that will answer your questions.
Yes, I meant closing the issue on github if your doubt is solved.