https://d2l.ai/chapter_recurrent-neural-networks/language-model.html
Unlike numpy.random.randint(a, b), Python’s standard random generator random.randint(a, b) generates integers in the range [a, b], that is b inclusive. So I think the code
corpus = corpus[random.randint(0, num_steps):]
should be
corpus = corpus[random.randint(0, num_steps - 1):]When training our neural network, a minibatch of such subsequences will be fed into the model. Suppose that the network processes a subsequence of 𝑛 time steps at a time. Fig. 8.3.1 shows all the different ways to obtain subsequences from an original text sequence, where 𝑛=5
Over here what does n signify the blocks or the number of characters in each block
Why are we subtracting 1 in the following
num_subseqs = (len(corpus) - 1) // num_steps
My guess is that can be avoided
We need to reserve 1 length for the label sequence,I guess.
Similarly for Sequential Paritioning, we need to add num_steps-1
def seq_data_iter_sequential(corpus, batch_size, num_steps): #@save
“”“Generate a minibatch of subsequences using sequential partitioning.”""
#Start with a random offset to partition a sequence
offset = random.randint(0, num_steps) # should be num_steps-1
Exercises and my errant answers
- Suppose there are 100, 000 words in the training dataset. How much word frequency and
multi-word adjacent frequency does a four-gram need to store?
what does multi word adjacent frequency mean? i reckon about 99,997 - 100000
-
How would you model a dialogue?
by taking out the speakers name, through putting in as the stop word, rest shouldbe the same.
-
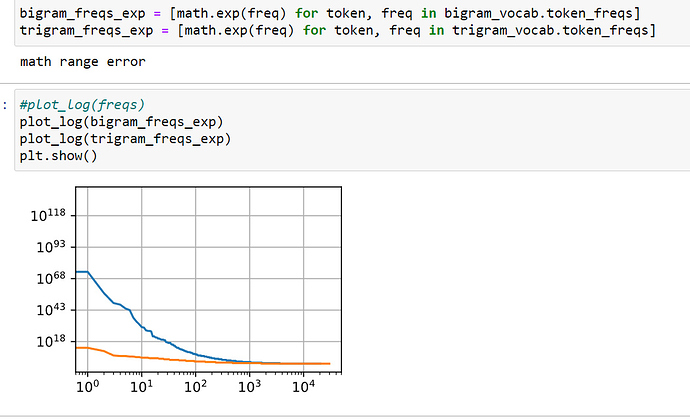
Estimate the exponent of Zipfʼs law for unigrams, bigrams, and trigrams.
okay.two decaying functions. Not able to make unigram.
https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0053227was this what we had to do?
-
What other methods can you think of for reading long sequence data?
maybe storing them in a dict,for oft repeated words memory can be saved
-
Consider the random offset that we use for reading long sequences.
-
Why is it a good idea to have a random offset?
Since the input prompt would be random model would be able to handle it better, otherwise the model might just learn from adjacent word sets.
-
Does it really lead to a perfectly uniform distribution over the sequences on the document?
It should.
-
What would you have to do to make things even more uniform?
Would maybe take subsequences based on some distribution.
-
-
If we want a sequence example to be a complete sentence, what kind of problem does this
introduce in minibatch sampling? How can we fix the problem?All the sentences have different number of words so we wont be able to get a minibatch that is uniform.
we can pad data.
Quick questions about the seq_data_iter_sequential code:
(1)
I noticed you generated the set of starting indices incrementing by the step size
indices = list(range(0, num_subsequences * step_size, step_size))
to ensure you do not go out of bounds when computing the subsequences in the offset in each batch
X = [corpus_offset[index:index + step_size] for index in indices_subset]
Doesn’t this limit the number of choices each sequence can have and skew the randomness to select tokens from that structured set of indices? Notice your indices are always
{ step_size*i : i = 0, 1, ..., len(offset) -1 }
which means some indices will start the sequence more often than others will. I think in the (list(range(35)), 2, 5) example, indices of the form 5*k ±{0,1,2} will be more likely to start the sequence.
(2)
You shuffle the indices and compute sliding windows of length batch_size. We choose to shift them by batch_size as determined by the for-loop.
for i in range(0, batch_size * num_batches, batch_size):
indices_subset = indices[i:i + batch_size] # sliding window shifted by batch size
Why do you choose to shift them by batch size instead of looping from 0 to num_batches? Does that choice matter?
For the sequential processing, why do we not keep the sequential subsequences in the same minibatch? For an example, currently if we check what do we get with the my_seq example, current implementation could return
X: tensor([[ 0, 1, 2, 3, 4], [17, 18, 19, 20, 21]])
in the first minibatch and
X: tensor([[ 5, 6, 7, 8, 9], [22, 23, 24, 25, 26]])
in the second minibatch.
Is there a reason we don’t use the following structure:
X: tensor([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9]]) # First minibatch
X: tensor([[10, 11, 12, 13, 14], [15, 16, 17, 18, 19]]) # Second minibatch
Great question!
but I think it will act as batch-size =1 since both subsequences you given are sequential .the exact answer should raise in the usage of next section.
additionally, this section confused me that it said laplace smoothing aimed at the low frequencies of tokens but it was overrun by following zipf’ law ![]()
for question #3, I think we can do a regression on the formula under the zipf’s law as per n-grams respectively, than the a and c will be derived automatically
@d2l.add_to_class(TimeMachine) #@save
def build(self, raw_text, vocab=None):
tokens = self._tokenize(self._preprocess(raw_text))
if vocab is None: vocab = Vocab(tokens)
corpus = [vocab[token] for token in tokens]
return corpus, vocab
corpus, vocab = data.build(raw_text)
len(corpus), len(vocab)
I think it’s
corpus, vocab = data.build(text)
instead of raw_text.
Perplexity can be best understood as the reciprocal of the geometric mean of the number of real choices that we have when deciding which token to pick next.
I suppose it should be:
“Perplexity, which is the reciprocal of the geometric mean of the (conditional) probabilities the language model assigns to each token in the sequence, can be best understood as the number of choices that we have when deciding which token to pick next.”
Hi, I’m wondering about the differences in how you define Laplace smoothing in eq. (9.3.6) and other authors (e.g. Jurafsky&Martin in their SLPed3, ch. 3.5.2). In the second line they would rather have
$$\hat{P}(x’ \mid x) & = \frac{n(x, x’) + \epsilon_2}{n(x) + \epsilon_2 m} $$
I do not really see a transformation from one to the other. Is there some other unreferenced source, on which you based this part of the chapter?
A better language model should allow us to predict the next token more accurately.
Thus, it should allow us to spend fewer bits in compressing the sequence.
So we can measure it by the cross-entropy loss averaged over all the $n$ tokens of a sequence:
$$
\frac{1}{n} \sum_{t=1}^n -\log P(x_t \mid x_{t-1}, \ldots, x_1)
$$
Hello,
As far as I know, for a discrete random variable $X$ with a probability distribution $ p(x)$, the entropy is defined as:
$$
H(p) = -\sum_{x} p(x) \log p(x)
$$
How could we decuce from this formula to obtain the cross-entropy loss averaged over all the $n$ tokens of a sequence defined as above?