https://d2l.ai/chapter_recurrent-neural-networks/language-model.html
Is there a way to calculate and actually quantify a value for excessive 1 in this section?
Is it bad when

This^ appears in the text?
Hi @smizerex, this equation render properly on my side. Could you refresh the page and let me know if it didn’t render at your side?
I meant to say “exercise 1” my bad.
Sequential Partitioning: why the input (X) and output (Y) data need to be adjacent?
Hi @nglelinh, great question. We are building a text generation model throughout this chapter, so the outputs are supposed to be the adjacent next few tokens for the inputs.
Improvement to max the randomness:
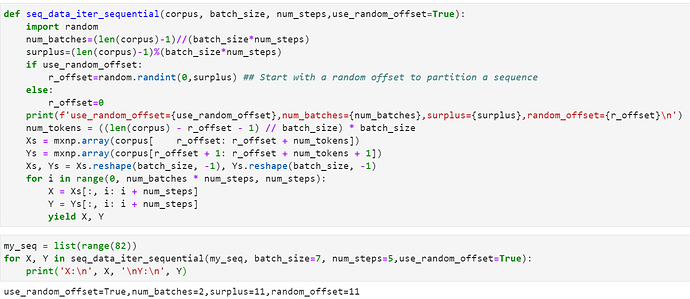
def seq_data_iter_sequential(corpus, batch_size, num_steps,use_random_offset=True):
import random
num_batches=(len(corpus)-1)//(batch_sizenum_steps)
surplus=(len(corpus)-1)%(batch_sizenum_steps)
if use_random_offset:
r_offset=random.randint(0,surplus) ## Start with a random offset to partition a sequence
else:
r_offset=0
print(f’use_random_offset={use_random_offset},num_batches={num_batches},surplus={surplus},random_offset={r_offset}\n’)
num_tokens = ((len(corpus) - r_offset - 1) // batch_size) * batch_size
Xs = mxnp.array(corpus[ r_offset: r_offset + num_tokens])
Ys = mxnp.array(corpus[r_offset + 1: r_offset + num_tokens + 1])
Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
for i in range(0, num_batches * num_steps, num_steps):
X = Xs[:, i: i + num_steps]
Y = Ys[:, i: i + num_steps]
yield X, Y
examles
my_seq = list(range(82))
for X, Y in seq_data_iter_sequential(my_seq, batch_size=7, num_steps=5,use_random_offset=True):
print(‘X:\n’, X, ‘\nY:\n’, Y)
Demo Images
For section 8.3, our aim is to predict next token given the previous sequence of token (“the target is to predict the next token based on what tokens we have seen so far”)
Why we shift the token by one offset (" hence the labels are the original sequence, shifted by one token."). For example, for X= [27,28, 29, 30, 31] expected Y should be [33,34,35,…] but we are taking a shifted offset. Why we are doing this, as we want to predict next token(s), which are 33, 34, and so on?
Both functions produce adjacent sequences based on the input. Textual sequences have a step size of 1 because we want directly adjacent words. In you case, you could gave it list(range(0,70,2)) and your example would work just fine.
@zhangjiekui I rewrote the author’s code to match yours,
def seq_data_iter_sequential(corpus, batch_size, step_size, use_random_offset=True):
num_batches=(len(corpus)-1)//(batch_size*step_size)
surplus=(len(corpus)-1)%(batch_size*step_size)
## Start with a random offset to partition a sequence
if use_random_offset:
index_offset = numpy.random.randint(low = 0, high = surplus -1)
else:
index_offset=0
num_tokens = ((len(corpus) - index_offset - 1) // batch_size) * batch_size
Xs = torch.tensor(corpus[index_offset : index_offset + num_tokens ])
Ys = torch.tensor(corpus[index_offset + 1: index_offset + num_tokens + 1])
Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
for i in range(0, num_batches * step_size, step_size):
X = Xs[:, i: i + step_size]
Y = Ys[:, i: i + step_size]
yield X, Y
def generate_sequence_batches_via_random_sampling(corpus, batch_size, step_size):
# Random offset to partition a sequence
index_offset = numpy.random.randint(low = 0, high = step_size)
num_subsequences = (len(corpus) - index_offset - 1) // step_size # Subtracting 1 accounts for labels
indices = list(range(0, num_subsequences * step_size, step_size))
numpy.random.shuffle(indices)
# Constructs the sliding window batches of length batch_size & shifted by batch_size
num_batches = num_subsequences // batch_size
for i in range(0, batch_size * num_batches, batch_size):
indices_subset = indices[i:i + batch_size] # sliding window shifted by batch size
# X has shape (batch_size, step_size)
X = [corpus[index + index_offset : index + index_offset + step_size ] for index in indices_subset]
Y = [corpus[index + index_offset + 1 : index + index_offset + step_size + 1] for index in indices_subset]
yield torch.tensor(X), torch.tensor(Y)
Even though the shape your outputs is the same, I think you’re missing the crucial step of shuffling the indices.