Exercises and my answers
- What happens if you change the dropout probabilities for the first and second layers? In
particular, what happens if you switch the ones for both layers? Design an experiment to
answer these questions, describe your results quantitatively, and summarize the qualitative
takeaways.
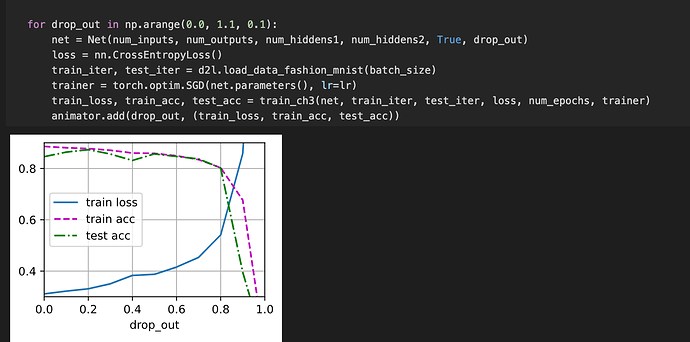
- Nothing much changes based on the final accuracy to compare. I compared for 10 epochs but no significant difference.
- Increase the number of epochs and compare the results obtained when using dropout with
those when not using it.
- there is no significant difference in loss. I am getting comparative results in both. (I am wondering if my implementation is faulty)
- What is the variance of the activations in each hidden layer when dropout is and is not applied? Draw a plot to show how this quantity evolves over time for both models.
- What is meant by variance here do we just apply torch.var over the net.linear weight layers? this is the graph I came up with. after getting variance in forward propogation of hidden layers.
- Why is dropout not typically used at test time?
- Because we would like all the features weights to be useful and consequential to making the prediction.
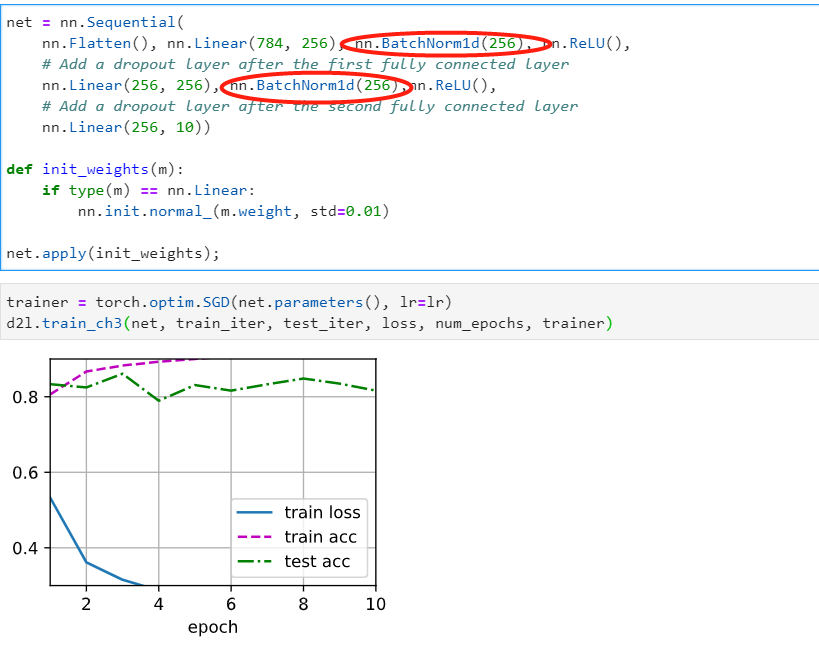
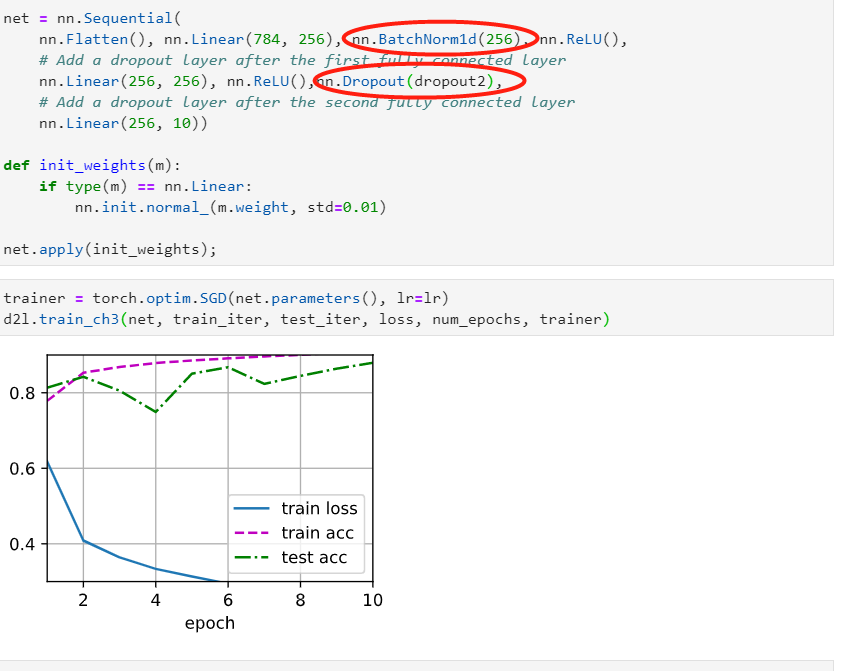
- Using the model in this section as an example, compare the effects of using dropout and
weight decay. What happens when dropout and weight decay are used at the same time?
Are the results additive? Are there diminished returns (or worse)? Do they cancel each other
out?
- The returns are diminished when using both, compared to using them individually.
- What happens if we apply dropout to the individual weights of the weight matrix rather than
the activations?
- it is still training. But with some slight oscillation in loss. This is the forward implementation
def forward(self, X):
out = self.lin1(X.reshape(-1,784))
out = dropout_layer(out, self.dropout1)
out = self.relu(out)
out = self.lin2(out)
out = dropout_layer(out, self.dropout2)
out = self.relu(out)
out = self.lin3(out)
return out
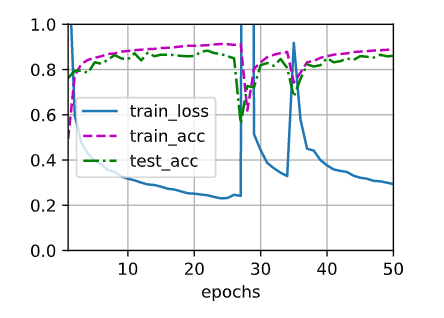
- Invent another technique for injecting random noise at each layer that is different from the
standard dropout technique. Can you develop a method that outperforms dropout on the
Fashion-MNIST dataset (for a fixed architecture)?
- I propose to add noise after each hidden layer.
class net_epsilon(nn.Module):
def __init__(self, num_inputs=784, num_outputs=10, num_hidden1=256, num_hidden2=256, epsilon_m=0.02, epsilon_d=0.02):
super(net_epsilon, self).__init__()
self.lin1 = nn.Linear(num_inputs, num_hidden1)
self.lin2 = nn.Linear(num_hidden1, num_hidden2)
self.lin3 = nn.Linear(num_hidden2, num_outputs)
self.relu = nn.ReLU()
self.epsilon_m = epsilon_m
self.epsilon_d = epsilon_d
self.num_inputs = num_inputs
def forward(self, X):
out = self.relu(self.lin1(X.reshape(-1,self.num_inputs)))
out = out + torch.normal(self.epsilon_m, self.epsilon_d, (out.shape))
out = self.relu(self.lin2(X.reshape(-1, self.num_inputs)))
out = out + torch.normal(self.epsilon_m, self.epsilon_d, (out.shape))
out = self.lin3(out)
- the results are not that promising though. The thing is the model predict well the losses are so close that you cant really conclude anything.