“Searching” is the best way to solve common questions like this.
Do you really want to learn? Or you only want to ask to act like a learner.
CNN: TODO:for you
RNN: http://preview.d2l.ai/d2l-en/master/chapter_recurrent-neural-networks/bptt.html
How about:
x = np.linspace(- np.pi,np.pi,100)
x = torch.tensor(x, requires_grad=True)
y = torch.sin(x)
z = y.sum()
z.backward()
d2l.plot(x.detach(),(y.detach(),x.grad),legend = (('sin(x)','grad w.s.t x')))My solution to the last exercise
import torch
import matplotlib.pyplot as plt
import numpy as np
import math
%matplotlib inline
x = torch.arange(0, 2*math.pi, 0.1)
x.requires_grad_(True)
y = torch.sin(x).sum().backward() #Derivando y respecto a x
dy_dx = x.grad
x = x.detach().numpy()
y = np.sin(x)
dy_dx = dy_dx.numpy()
fig = plt.figure()
plt.plot(x, y, ‘-’, label = ‘y = sin(x)’)
plt.plot(x, dy_dx, ‘–’, label =’ dy_dx = cos(x)’)
plt.axis(‘equal’)
leg = plt.legend();
x = torch.arange(-np.pi, np.pi, 0.1, requires_grad=True)
y = torch.sin(x)
y.sum().backward()
x.grad
Exercise 1. The second derivative is much more expensive because, for a function f with n variables, the Hessian Matrix has n² elements while the gradient vector has n elements. In other words, there are n² possible second order derivatives ( ∂²f/∂x1², ∂²f/∂x1∂x2, …) while there are n possible first order derivatives (∂f/∂x1, ∂f/∂x2, …, ∂f/∂xn).
Backward for Non-Scalar Variables:
Seems, in the text, by calculating y.backward(torch.ones(len(x))), we contract the Jacobian over the 4 components of y(x). The Jacobian is a 4x4 matrix. I can extract each column via y.backward(torch.tensor([1,0,0,0])), #where i shift the 1 to each of the 4 column slots.
Is this best way to calculate the Jacobian?
My anwser for ex 2 3 4,welcom to tell me if you find any error
'''
ex.2
Aafter running the function for backpropagation, immediately run it again and see what hap-
pens. Why?
reference:
[https://blog.csdn.net/rothschild666/article/details/124170794](https://blog.csdn.net/rothschild666/article/details/124170794)
'''
import torch
x = torch.arange(4.0, requires_grad=True)
x.requires_grad_(True)
y = 2 * torch.dot(x, x)
y.backward(retain_graph=True)#need to set para = Ture
y.backward()
x.grad
out for ex2:
tensor([ 0., 8., 16., 24.])
'''
ex.3
In the control flow example where we calculate the derivative of d with respect to a, what
would happen if we changed the variable a to a random vector or a matrix? At this point, the
result of the calculation f(a) is no longer a scalar. What happens to the result? How do we
analyze this?
reference:
[https://www.jb51.net/article/211983.htm](https://www.jb51.net/article/211983.htm)
'''
import torch
def f(a):
b = a * 2
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
a = torch.randn(size=(2,3), requires_grad=True)
#a = torch.tensor([1.0,2.0], requires_grad=True)
print(a)
d = f(a)
d.backward(d.detach())#This is neccesary, I don't know why, is it because there are b and c in the function?
#d.backward()#wrong
print(a.grad)
out for ex3:
tensor([[-0.6848, 0.2447, 1.5633],
[-0.1291, 0.2607, 0.9181]], requires_grad=True)
tensor([[-179512.9062, 64147.3203, 409814.3750],
[ -33844.5430, 68346.7969, 240686.7344]])
'''
ex.4
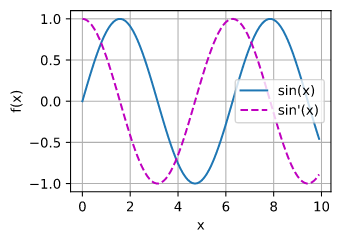
Let f (x) = sin(x). Plot the graph of f and of its derivative f ′ . Do not exploit the fact that
f ′ (x) = cos(x) but rather use automatic differentiation to get the result.
'''
#suppose the functions in 2.4.2Visualization Utilities has been constructed in d2l
from d2l import torch as d2l
x = d2l.arange(0,10,0.1, requires_grad = True)
y = d2l.sin(x)
y.backward(gradient=d2l.ones(len(y)))#y.sum().backward() can do the same thing
#.detach.numpy() is needed because x is set to requires_grad = True
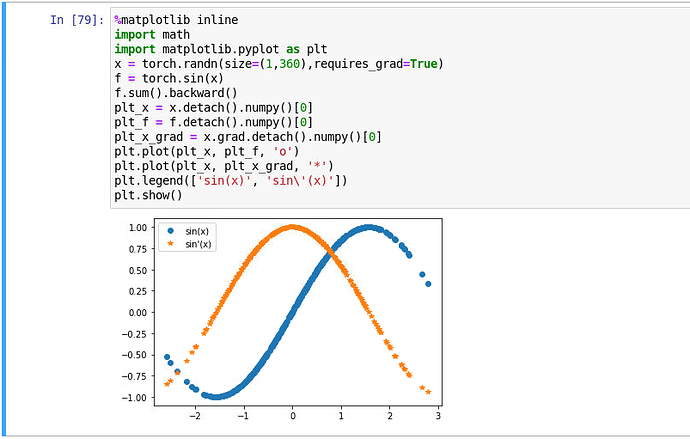
d2l.plot(x.detach().numpy(), [y.detach().numpy(),x.grad], 'x', 'f(x)', legend = ['sin(x)','sin\'(x)'])
out for ex4:
Can someone please explain the result of 2.5.1 to me. I understand how the first function is just y = 2x^2, but creating the new function that is y = x.sum(), just returns 6. Is this conceptually 6x or is it just 6 or is this just x (i’m assuming the third because that’s the only way we can get 1 as the gradient all the time) or am i missing something?
My understanding about 2.5.1’s pytorch code blocks:
y = x.sum() is just a way of defining a computational graph in PyTorch, which means evaluating each component of x and adding them up. Gradients are computed on each component of x, NOT on the y graph. Evaluating gradient on a component of x means computing for y_i = x_i (which yields 1).
The same principal applies to the y = 2 * x^Tx part, y is NOT 2x^2, it’s a computational graph for evaluating 2 * x^Tx where each component of it is actually y_i = 2 * x_i * x_i. So the graph y is in fact sum { 2 * x_i * x_i }.
HTH
Can someone help with Questions 5 and 6. Is this a pen-paper question, writing down backprop for the computation graph, or is this supposed to be implemented (if yes, then can someone elaborate more on it or provide a solution.)
Also problems 7, 8 are difficult ones, but at least there is a good resource provided by Denis Kazakov.
Hi! In Exercise 5, I don’t understand why my solution and the expected derivative do not correspond:
%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l
import math
x = torch.linspace(0.1, 10, 100)
x.requires_grad_(True)
def f(x):
return ((torch.log(x ** 2)) * torch.sin(x)) + (x ** -1)
y = f(x)
y.backward(torch.ones_like(y))
p = x.grad
Plot the function and its derivative
plt.plot(x.detach().numpy(), y.detach().numpy(), label=‘f(x)’)
plt.plot(x.detach().numpy(), p.detach().numpy(), label=“f’(x)”)
plt.xlabel(‘x’)
plt.ylabel(‘y’)
plt.legend()
plt.grid(True)
plt.show()
gives me this plot:
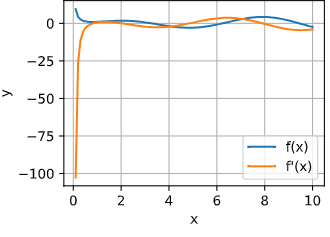
and when I compare
desired_derivative = -(2 / x) * torch.sin(x) + torch.log(x**2) * torch.cos(x) - (1/x **2)
p == desired_derivative
it evaluates to False.
Can you help me?
Ex2.
import torch
x = torch.arange(4.0)
x.requires_grad_(True)
y = x @ x
y.backward()
Output (second run):
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
/tmp/ipykernel_82/1055444503.py in <module>
----> 1 y.backward()
/opt/miniconda/lib/python3.7/site-packages/torch/_tensor.py in backward(self, gradient, retain_graph, create_graph, inputs)
394 create_graph=create_graph,
395 inputs=inputs)
--> 396 torch.autograd.backward(self, gradient, retain_graph, create_graph, inputs=inputs)
397
398 def register_hook(self, hook):
/opt/miniconda/lib/python3.7/site-packages/torch/autograd/__init__.py in backward(tensors, grad_tensors, retain_graph, create_graph, grad_variables, inputs)
173 Variable._execution_engine.run_backward( # Calls into the C++ engine to run the backward pass
174 tensors, grad_tensors_, retain_graph, create_graph, inputs,
--> 175 allow_unreachable=True, accumulate_grad=True) # Calls into the C++ engine to run the backward pass
176
177 def grad(
RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
- The
.backward()call will automatically free all the intermediate tensors in a computational graph after the backprop. - In that sense, “double backward” can not be realized unless one specifies
retain_graph=True.
Ex3.
def f(a):
b = a * 2
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
a = torch.randn(size=(4, ), requires_grad=True)
d = f(a)
d.backward()
Output:
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
/tmp/ipykernel_82/535593037.py in <module>
1 a = torch.randn(size=(4, ), requires_grad=True)
2 d = f(a)
----> 3 d.backward()
/opt/miniconda/lib/python3.7/site-packages/torch/_tensor.py in backward(self, gradient, retain_graph, create_graph, inputs)
394 create_graph=create_graph,
395 inputs=inputs)
--> 396 torch.autograd.backward(self, gradient, retain_graph, create_graph, inputs=inputs)
397
398 def register_hook(self, hook):
/opt/miniconda/lib/python3.7/site-packages/torch/autograd/__init__.py in backward(tensors, grad_tensors, retain_graph, create_graph, grad_variables, inputs)
164
165 grad_tensors_ = _tensor_or_tensors_to_tuple(grad_tensors, len(tensors))
--> 166 grad_tensors_ = _make_grads(tensors, grad_tensors_, is_grads_batched=False)
167 if retain_graph is None:
168 retain_graph = create_graph
/opt/miniconda/lib/python3.7/site-packages/torch/autograd/__init__.py in _make_grads(outputs, grads, is_grads_batched)
65 if out.requires_grad:
66 if out.numel() != 1:
---> 67 raise RuntimeError("grad can be implicitly created only for scalar outputs")
68 new_grads.append(torch.ones_like(out, memory_format=torch.preserve_format))
69 else:
RuntimeError: grad can be implicitly created only for scalar outputs
- Since
aas well asdis no longer a scalar, we need to reducedto make backprop feasible.
d.sum().backward()
a.grad == d / a
Output:
tensor([True, True, True, True])
Ex4-5.
- The dependency graph (computational graph):
- Applying the backprop algorithm according to the chain rule…
- The
+operationy = n1 + n2:n1.grad = 1, n2.grad = 1 - The inverse operation
n1 = 1 / x:x.grad1 = (- 1 / x ** 2) * n1.grad = - 1 / x ** 2 - The
*operationn2 = n3 * n4:n3.grad = n4 * n2.grad = log(x ** 2), n4.grad = n3 * n2.grad = sin(x) - The
sinoperationn3 = sin(x):x.grad2 = cos(x) * n3.grad = cos(x) * log(x ** 2) - The
logoperationn4 = log(n5):n5.grad = 1 / n5 * n4.grad = 1 / x ** 2 * sin(x) - The square operation
n5 = x ** 2:x.grad3 = 2 * x * n5.grad = 2 / x * sin(x) - Final result:
x.grad = x.grad1 + x.grad2 + x.grad3 = - 1 / x ** 2 + cos(x) * log(x ** 2) + 2 / x * sin(x)
- The
import torch
torch.manual_seed(713)
x = torch.randn(size=(), requires_grad=True)
n1, n3, n5 = 1 / x, torch.sin(x), x ** 2
n4 = torch.log(n5)
n2 = n3 * n4
y = n1 + n2
y.backward()
x.grad, - 1 / x ** 2 + torch.cos(x) * torch.log(x ** 2) + 2 / x * torch.sin(x)
Output:
(tensor(-1.7580), tensor(-1.7580, grad_fn=<AddBackward0>))
I’m probably too late for you, but posting here for posterity.
Firstly, you need to use torch.log10(x**2) in your f(x) function, as just “log” function is for natural logarithm, and we’re given “log base 10” in question. And for the same reason I guess, you’ve mistakenly calculated derivative considering natural log of x squared. I’m leaving the code below with correct derivative.
from d2l import torch as d2l
x = torch.linspace(0.1, 10, 100)
x.requires_grad_(True)
def f(x):
return ((torch.log10(x ** 2)) * torch.sin(x)) + (x ** -1)
y = f(x)
y.backward(torch.ones_like(y))
p = x.grad
d2l.plot(x.detach(), [y.detach(), p], 'x', 'f(x)', legend=['f(x)', 'df/dx'])
z=4
desired_derivative = (2 / (x * torch.log(torch.tensor(10)))) * torch.sin(x) + torch.log10(x**2) * torch.cos(x) - (1/x **2)
print(f"{(p[z]-desired_derivative[z]).detach().numpy():.18f}")
p == desired_derivative, p[z], desired_derivative[z], p[z] == desired_derivative[z]
You might get some “False” values when comparing AD and desired derivative results, but those are just because of unreliable floating point math of computers.
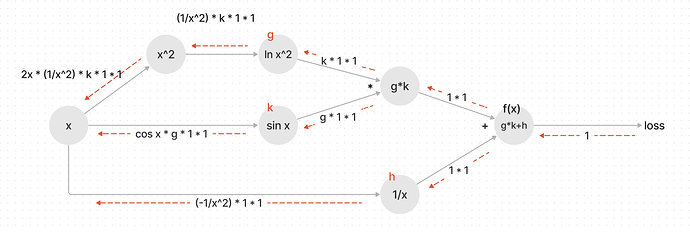
One more diagram for 2.5.6.5 and 2.5.6.6.
I had to get really explicit with the steps but this helped me out, maybe it’ll help someone else out too.
- Assuming we’re talking about the derivative of a scalar with respect to a tensor, the first derivative will be of the same size as the tensor. But the second derivative will be of that size, squared! Further, autodiff only requires a single backward pass to find the gradients - but if we want to find the full Hessian, we then need to find the derivative of each component of our initial gradients. So you’d have to a full backwards pass for every parameter, or find a more efficient way of computing this.
- When you run
.backward()multiple times, the gradients accumulate (are added to each other). - The shape of
f(a)will match the shape ofa, so ifais a vector or matrix, we’ll need to call something like.sum().backward()or.backward(torch.ones_like(d)). Once we do,a.grad == d / awill yield a tensor of the same shape asa, with allTruevalues. - See the code below:
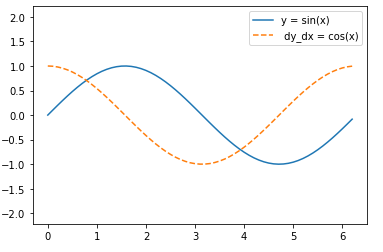
import torch
import matplotlib.pyplot as plt
x = torch.linspace(-5, 5, 100, requires_grad=True)
y = torch.sin(x)
y.sum().backward()
plt.plot(x.detach(), y.detach())
plt.plot(x.detach(), x.grad.detach())
plt.legend(["sin(x)", "dy/dx sin(x)"])
print((x.grad == torch.cos(x)).all())
Questions 5-7
I did these on paper by hand. For anyone having a hard time with questions 5-7, I recommend working through this tutorial from Andrej Karpathy.
Question 8
I tried doing forwardprop by hand on a number of computational graphs. For each input, one has to perform a full forward pass through the graph. In contexts where we’d like to track the gradient of some output with respect to one or a few specific inputs, forwardprop makes sense! It would also make sense in any context where we have N inputs and M outputs, and N << M. In practice, neural networks have a massive number of inputs and a scalar output loss, making backwards differentiation the obvious choice. A rule of thumb is that the forward-mode cost is proportional to the number of inputs, and the backward-mode cost is proportional to the number of outputs.
Other tradeoffs may come up in practice, depending on the layout of your computational graph. For example, backprop starts off at a scalar, and the computational graph fans out from there. You might think this makes it difficult to parallelize early parts of the graph, but in practice, backprop parallelizes very well. One might think that forwardprop would be easier to parallelize (since you can start out propogating from all inputs in parallel), but you could get weird dependency bottlenecks as different branches have to be “merged” deeper into the network: if branch A from input a and branch B from input b must be multiplied together, and branch A is very fast to propogate through but branch B is very slow to propogate through, branch A will be bottlenecked by branch B. Generally, you’ll be bottlenecked by the slowest path through the network.
Another tradeoff is memory usage: backprop requires storing intermediate activations from the forward pass, meaning memory usage scales with the depth of a network. Forwardprop doesn’t have this requirement! Aside from tracking the partial derivatives at each step, forwardprop stateless as we move through the network, meaning the memory footprint is generally much smaller.
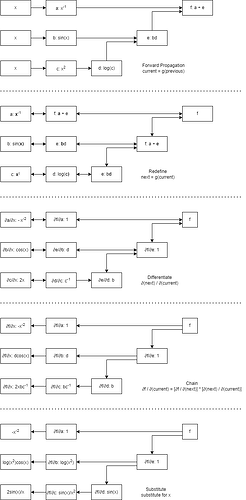
I have provided a diagram created using Mermaid that illustrates the detaching computation sections.
The solid lines represent the forward computation path, while the dashed lines indicate the backpropagation path.
I hope this helps you better understand the workflow of this functionality. Please let me know if there are any issues or corrections needed.